Burgers PDE with piecewise constant initial condition

Question

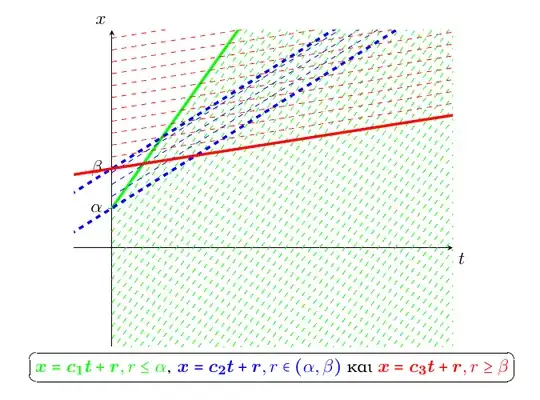
Let's deal with this Burgers PDE:

$$\left\lbrace \begin{aligned} &u_t + uu_x = 0, \quad x\in \Bbb{R}, t>0\\ &u(x,0) = \varphi(x) \end{aligned} \right. $$

where

$$\varphi(x) = \left\lbrace \begin{aligned} &c_1, \quad x\leq \alpha\\ &c_2, \quad \alpha\leq x\leq \beta, \quad c_1> c_2> c_3 .\\ &c_3, \quad x\geq \beta \end{aligned} \right. $$

You can see the characteristic curves below:

1. I believe the breaking time is $\boldsymbol{t_b=0}$, because it is the $\inf$ of $t$-coordinates of the intersection points of characteristics curves. Am I right?
2. How can I find the weak solution? How can I find the discontinuity line? At $t=0$ we have $x=\alpha$ and $x=\beta$ at the intersection points.

Thanks, in advance!

Answer 1

Apply the techniques in this post. Because $c_1>c_2>c_3$, the solution for small time will be shock waves whose speed is deduced from the Rankine-Hugoniot condition $$ s_{12} = \tfrac12(c_1+c_2)> c_2, \qquad s_{23} = \tfrac12(c_2+c_3) < c_2. $$ Hence, for small times, $$ u(x,t) = \left\lbrace \begin{aligned} &c_1 , & & x\leq \alpha + s_{12} t\\ &c_2 , & & \alpha + s_{12} t \leq x\leq \beta + s_{23} t\\ &c_3 , & & x\geq \beta + s_{23} t \end{aligned} \right. $$ Waves of amplitude $c_1$, $c_3$ will interact at some time $t^*>0$ if $$ \alpha + s_{12} t^* = \beta + s_{23} t^* = x^*, $$ i.e., at the time $$ t^* = \frac{\beta -\alpha}{s_{12}-s_{23}} > 0 $$ and position $$ x^* = \frac{s_{12}\beta-s_{23}\alpha}{s_{12}-s_{23}} . $$ This is very much possible since $\beta -\alpha \geq 0$ and $s_{12}-s_{23}>0$. The resulting shock wave has Rankine-Hugoniot speed $s_{13} = \frac12(c_1+c_3)$, and we have $$ u(x,t) = \left\lbrace \begin{aligned} &c_1 , & & x\leq x^* + s_{13} t\\ &c_3 , & & x\geq x^* + s_{13} t \end{aligned} \right. $$ for $t>t^*$.