2

I'm having trouble deciding what the antiderivative of $f(x)=\frac{1}{5-3\cos x}$ is. On the one hand, it is tempting to say it is $F(x)=\frac{1}{2} \arctan (2\tan \frac{x}{2})$. However, this would make the Second Fundamental Theorem of Calculus invalid, since $f$ is integrable on $[0,2\pi]$ but apparently $\int_0^{2\pi} f(x) dx \neq F(2\pi)-F(0)=0$.

Clearly $f$ is continuous so it must have an antiderivative, what is it?

Moronic
  • 167
  • 4
    https://math.stackexchange.com/questions/1942983/find-int-02-pi-frac15-4-cos-x-dx/1943009#1943009 In short: the Weierstrass substitution has a well known downside, it's only valid on an interval. Indeed, it produces a periodic function, even when the integrand is positive (hence the antiderivative is increasing and certainly not periodic). – Jean-Claude Arbaut Dec 11 '22 at 22:13

2 Answers2

1

Here's a graph of the antiderivative $F(x)$:

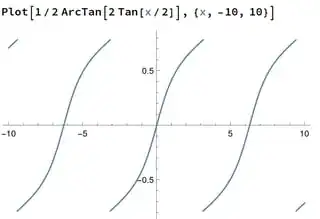
plot of F(x)

You can see the function is periodic and discontinuous. In particular it'll have jumps at $\pm \pi, \pm 3 \pi, \pm 5 \pi$, etc since those are the points where $\tan(\frac x 2)$ jumps from $+ \infty$ to $- \infty$.

The second part of the F.T.C. includes a requirement that $F$ must be continuous on the interval we care about. That means you can't just plug in $0$ and $2 \pi$, since those are not in the same "continuous segment" of $F$. Another way of saying this is: $F$ is not a valid antiderivative of $f$ on any interval that contains one of these discontinuities.

Instead, once you see where $F$ is continuous, you could rewrite your integral as $\int_{-\pi}^{\pi} f(x) dx$ (using the fact that your integrand is periodic) and then evaluate as $$\lim_{x \to \pi^-} F(x) - \lim_{x \to -\pi^+} F(x) = \left( \frac \pi 4 \right) - \left( - \frac \pi 4 \right) = \frac \pi 2$$

which is the correct value for this definite integral.

If you don't want to use the "periodicity trick", then an alternate strategy is to "break the integral up into chunks so $F$ is continuous on each chunk". $$ \begin{align} \int_0^{2 \pi} f(x) dx &= \int_{0}^\pi f(x) dx + \int_\pi ^{2 \pi} f(x) dx \\ &= \left[\lim_{x \to 0^-} F(x) - \lim_{x \to -\pi^+} F(x) \right] + \left[\lim_{x \to \pi^-} F(x) - \lim_{x \to 0^+} F(x) \right] \\ &= \left[ \frac \pi 4 - 0 \right] + \left[ 0 - \left(-\frac \pi 4\right) \right] \\ &= \frac \pi 2. \end{align} $$

This takes a couple of extra steps, but it's also more straightforward: you don't need to rely on noticing $f$ is periodic, you just need to know where $F$ is discontinuous.

David Clyde
  • 5,399
  • 1
    That's not the antiderivative of $f(x)$. It's not even continuous, let alone differentiable. – jjagmath Dec 12 '22 at 01:58
  • @jjagmath That's right: $F$ is a valid antiderivative of $f$ on any interval where $F$ is continuous, but $F$ is not a valid antiderivative on any interval that contains one of the discontinuities. I've edited the answer to state this more clearly. – David Clyde Dec 12 '22 at 02:05
  • @jjagmath How does this differentiation occur? Also, the floor function in your answer is effectively a constant making both answers be valid except at discontinuous points after differentiating to check. – Тyma Gaidash Dec 12 '22 at 03:24
  • 1
    @TymaGaidash Your original function $F$ satisfies $F'(x) = f(x)$ except at the discontinuities. However, to apply FTC2 you need $F$ to be a valid antiderivative on the whole interval you care about. That's why you need some extra trick - either the one I used or the one jjagmath used. – David Clyde Dec 12 '22 at 03:28
  • 1
    @TymaGaidash Stop using WolframAlpha as a reference. It's based on Mathematica, and both are very useful tools, but far from be rigorously, mathematically correct (I have a Mathematica notebook with a list of about 30 errors I've collected) – jjagmath Dec 12 '22 at 03:56
  • My take is that their use of computer tools is totally appropriate here: Use the tool, but then sanity check the results, and if you get something that doesn't make sense then think further or ask people questions until you do understand. This path will lead to better mathematical understanding. The problem is just when people trust the computer result blindly without checking whether it makes sense. – David Clyde Dec 12 '22 at 04:01
1

You can consider $F(x)=\frac{1}{2} \arctan (2\tan \frac{x}{2})$ as an antiderivative in the interval $(-\pi,\pi)$. Then with a little effort, extend it to an antiderivative in $\Bbb R$:

$$F(x) = \begin{cases} \frac{1}{2} \arctan (2\tan \frac{x}{2}) + \frac{\pi}{2}\lfloor\frac{x}{2\pi}+\frac{1}{2}\rfloor \text{ if } x\not\in \pi\Bbb Z\\ \frac{x}{4} \text{ if } x \in \pi\Bbb Z \end{cases}$$

See here

jjagmath
  • 22,582