Where does this approximation for $2^x-1$ come from?

Question

I found this fairly good approximation for $2^x-1$ while reverse-engineering a fast exp2f() C++ (undocumented, uncommented) implementation:

$$2^x-1\approx \frac{27.7280233}{4.84252568 - x} -0.49012907 x -5.7259425$$

This approximation is accurate for $x$ in $[0,1]$ and it is quite so (about 4 decimal digits). However I never found it mentioned anywhere. It is simply a hyperbole shifted linearly which fits $2^x-1$ in that range very nicely. I tried to google around for "rational exp2 approximation", "fractional exponential base two approximation" or with similar keywords, but I found nothing relevant to it.

Does anybody know where it comes from and whether it has a name ?

My curiosity is not just academical, I wanted to know where it come from just to understand whether it can be extended with more terms to improve its approximation accuracy. I know I can approximate $2^x$ or $2^x-1$ in that or another range by polynomial approximation, but they usually requires several terms, while this formula without any powers higher than one and one fraction does a very nice job, comparable more or less to a 4th degree polynomial!

Thanks

Answer 1

When you make a change of variable to express $e^x-1$ instead, you get a formula close to the local (near $0$) approximation $\dfrac{x^2/\sqrt2+(2+\sqrt2)x}{2+\sqrt2-x}$.

However, your formula is much better near $1$, and the error is uniformly small on $[0,1]$ and oscillating. Therefore I suspect some kind of minimax rational approximation (Remez). However, Remez is slightly better overall, but your formula is better near $0$, so the minimax approximation has been tuned to be good near $0$, which is desirable, as this function is probably often used for small arguments.

Below, the error with your function (blue) and Remez approximation (red). The Remez approximation was computed with Maple, with a numerator of degree $2$ and a denominator of degree $1$.

We can do better: Maple allows a weight on the error. With a weight $1000$ for $|x|<10^{-8}$ and $1$ otherwise, we get the approximation

$$\frac{ 27.704226690769845416}{4.8416702244134115171-x}- 0.48942480030516666506 x - 5.7220391320516093836$$

As you can see it's quite close to your formula.

Here is the error, again your function in blue and the Remez approximation in red:

It's possible to get a result even closer to your function by adjusting weights also at $1$ and $1/2$:

Answer 2

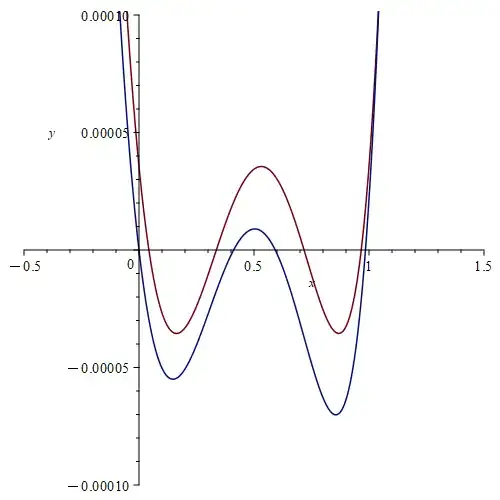
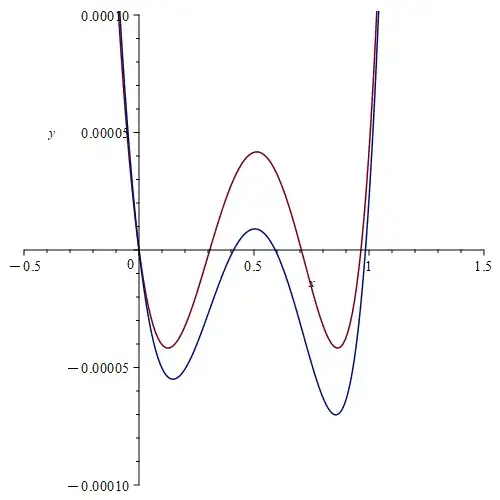
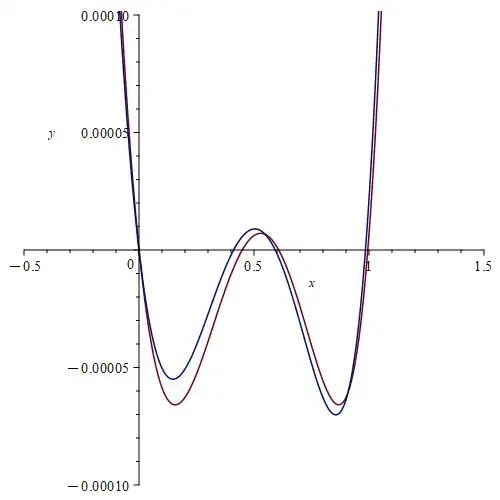
The approximation in the question is a particular arrangement of a rational approximation, and other answers have already explained how these can be derived from Padé approximants or with the Remez algorithm for creating minimax approximations. I could not find this particular approximation in a search of relevant literature going back to the 1950s. Searching for the coefficients on the internet, I did however trace it back to a 2011 blog post by Paul Mineiro, and the description there indicates that he derived this approximation himself (see the section "A Fast Approximate Exponential").

In general, a rational approximation $\mathrm{R}_{m,n}(x)=\frac{\mathrm{P}_{m}(x)}{\mathrm{P}_{n}(x)}$, where $\mathrm{P}_{n}$ denotes a polynomial of degree $n$, tends to have an approximation error smaller than a polynomial approximation $\mathrm{P}_{n+m}$. This is one reason rational approximations were very popular in the past, up to about the early 1990s. With processors of the 1950s through the 1980s, floating-point division was often not much slower than floating-point multiplication. For example, on the IBM 7090 a floating-point multiply executed in 16.8 to 40.8 microseconds, while a floating-point divide executed in 43.2 microseconds. On the Intel 8087, a floating-point multiply required 90-145 cycles, while a divide required 193-203 cycles (according to the 1987 Microsoft Macro Assembler 5.0 Reference).

Subsequent work on computer hardware focused on making multiplication very fast, then added the fused multiply-add operation, or FMA, which can execute a multiply and a dependent add in almost the same time as a plain multiply. Speeding up floating-point division is a much harder problem, such that modern processors provide division at a throughput on the order of $\frac{1}{10}$ to $\frac{1}{20}$ of that of multiplication. As a consequence, many modern approximations used for mathematical functions tend to be FMA-accelerated polynomial minimax approximations.

Rational approximations can also present problems when one tries to implement faithfully-rounded implementations of mathematical functions with error of at most 1 ulp, as they accumulate error from two polynomial evaluations plus a division. The accuracy standards for math libraries prior to the 1990s were less strict, often allowing several ulps of error and focusing instead on minimizing the number of numerical constants and the number of operations as both RAM and ROM were very small. Rational approximations could often be rearranged to achieve these objectives.

An example is the following approximation (I tweaked the coefficients to get closer to a minimax approximation) to $2^{x}-1$ on $[-1,1]$ crafted by Hirondo Kuki in 1964, using a truncated version of Gauss' continued fraction expansion for $e^{x}$ as a starting point (H. Kuki, Mathematical Functions - A Description of the Center's 7094 Fortran II Mathematical Function Library, University of Chicago Computation Center Report, February 1966, p. 54):

$$2^{x}-1 \approx \frac{2x}{c x^{2} - x + d - \frac{b}{x^{2}+a}}\ \ ,$$

where the values of the constants are $a=87.417032155030128$, $b=617.97007676566318$, $c=0.03465679176500755$, and $d=9.954608304921436$. The maximum relative error of this approximation is $\lt 1.7\cdot10^{-10}$. This level of accuracy is achieved with just nine operations (five additions, two multiplications, and two divisions) and four stored floating-point constants.

A particularly efficient arrangement for a rational approximation to $2^x-1$ inspired by the Padé approximants for $\exp(x)$ is

$$\mathrm{R}_{m,n}(x) := \frac{2x\mathrm{P}_{m}\left(x^{2}\right)}{\mathrm{Q}_{n}\left(x^{2}\right)-x\mathrm{P}_{m}\left(x^{2}\right)}$$

where $\mathrm{P}_{m}$ is a polynomial of degree $m$ and $\mathrm{Q}_{n}$ is a polynomial of degree $n$. In the 1990s I used an approximation $\mathrm{R}_{3,3}$ of this type to implement the instruction F2XM1 in the AMD Athlon processor. $\mathrm{R}_{1,2}$ for $2^{x}-1$ on $[-1, 1]$ uses $\mathrm{P}_{1}(x^{2}) := 28.937286906710295 x^2 + 2532.7737162012545$ and $\mathrm{Q}_{2}(x^{2}) := \left(x^{2} + 376.0928489774704\right) x^{2} + 7308.0401603051168$ and approximates the target function with a relative error $\lt 2.7\cdot 10^{-11}$ using ten operations.

Answer 3

If you reduce to same denominator, the expression is the ratio of a polynomial of degree $2$ to a polynomial of degree $1$ in $x$. This is like a $[2,1]$ Padé approximant.

Developed around $x=\frac 12$, this Padé approximant is $$2^x-1=\frac{(\sqrt{2}-1 )+\frac{1}{3} \left(1+2 \sqrt{2}\right) \log (2)\left(x-\frac{1}{2}\right)+\frac{\log ^2(2)}{3 \sqrt{2}}\left(x-\frac{1}{2}\right)^2} {1-\frac{1}{3} \log (2)\left(x-\frac{1}{2}\right)}=f(x)$$ whose error is $\frac{\log ^4(2)}{36 \sqrt{2}}\left(x-\frac{1}{2}\right)^4$ (at the bounds, this is $2.8\times 10^{-4}$).

Computing the norm $$\Phi(x)=\int_0^1\Big[2^x-1-f(x)\Big]^2 \,dx=1.00355\times 10^{-8}$$

Written as $$\frac{a}{b-x}- c x-d$$ we then have $$a=\frac{27}{\sqrt{2} \log (2)}=27.5438\qquad\qquad b=\frac{6+\log (2)}{2 \log (2)}=4.82809$$ $$c=\frac{\log (2)}{\sqrt{2}}=0.490129\qquad\qquad d=1+\frac{7}{\sqrt{2}}-\frac{\log (2)}{2 \sqrt{2}}=5.70468$$ which are quite close to the number you posted.

However, in terms of Padé approximant, this is not the good one since, as a series $$2^x-1=(\sqrt{2}-1)+\sqrt{2} \log (2)\left(x-\frac{1}{2}\right)+\frac{\log ^2(2)}{\sqrt{2}}\left(x-\frac{1}{2}\right)^2+O\left(\left(x-\frac{1}{2}\right)^3\right)$$

Since there is a constant term, the best Padé approximants are the $[n,n]$ ones; so, what is given is a compromise. Much better would be $$2^x-1=\frac{(\sqrt{2}-1)+ \frac{1}{2} \left(1+\sqrt{2}\right) \log (2)\left(x-\frac{1}{2}\right)+\frac{1}{12} \left(\sqrt{2}-1\right) \log ^2(2)\left(x-\frac{1}{2}\right)^2} {1-\frac{\log (2)}{2} \left(x-\frac{1}{2}\right)+\frac{\log ^2(2)}{12}\left(x-\frac{1}{2}\right)^2}=g(x)$$ whose error is $\frac{\log ^5(2)}{360 \sqrt{2}}\left(x-\frac{1}{2}\right)^5$ (at the bounds, this is $9.8\times 10^{-6}$).

Computing the norm $$\Phi(x)=\int_0^1\Big[2^x-1-g(x)\Big]^2 \,dx=1.07430\times 10^{-11}$$ which is $1,000$ times smaller that the previous one.

Edit

Let $P_n$ be the $[n,n]$ Padé approximant of $(2^x-1)$ and consider the norm $$\Phi_n=\int_0^1\Big[2^x-1-P_n)\Big]^2 \,dx$$

$$\left( \begin{array}{cc} n & \log_{10}(\Phi_n) \\ 1 & -5.37398 \\ 2 & -10.9689 \\ 3 & -17.2350 \\ 4 & -23.9801 \\ 5 & -31.0984 \\ 6 & -38.5290 \\ \end{array} \right)$$

A quick and dirty nonlinear regression for $$\log_{10}(\Phi_n)=a +b \,n^c$$ gives

$$\begin{array}{|lllll} \hline \text{} & \text{Estimate} & \text{Std Error} \\ a & -1.13967 & 0.006378 \\ b & -4.23261 & 0.004127 \\ c & +1.21591 & 0.000474 \\ \end{array}$$

Answer 4

I would recommend, if high accuracy is not very important, the following, easy manageable approximation:

$$2^{x}-1 \approx x+3\left(\frac{2}{\ln 2}-3\right)x(1-x)$$

Maximum approximation error here is about $0.004$

Average approximation error here is about $0.003$

The advantage of this approximation is that it can be used in approximate analytical calculations.

Say we need to compute the following integral:

$$\int_{0}^1\frac{2^{x}-1}{x}dx$$

With this approximation the approximate value of the integral is easy to calculate in closed form.