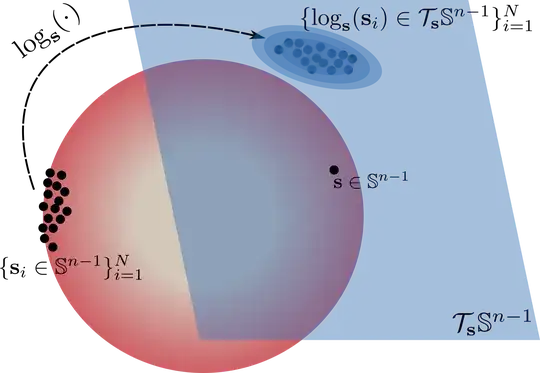
Let $\mathbb{S}^n$ be the $n$-sphere and let $\mathbf{s}\in\mathbb{S}^n$ be a point on the it. Also, let $\mathcal{S}=\{\mathbf{s}_i\in\mathbb{S}^n\colon \mathbf{s}_i\neq \mathbf{s}, i=1,\ldots,N\}$ be a set of $N$ point on the $n$-sphere different than $\mathbf{s}$.
My goal is to define a distance metric that would measure distance between the point $\mathbf{s}$ and the points in $\mathcal{S}$ similar to what the Mahalanobis distance would measure if the points where not distributed on the surface of the $n$-sphere but on a "flat", Euclidean space. In that case I would calculate the Mahalanobis distance using the sample mean and covariance of $\mathcal{S}$.
My attempts so far are as follows.
Let $\mathcal{T}_{\mathbf{s}}\mathbb{S}^n$ denote the tangent space on $\mathbf{s}\in\mathbb{S}^n$ and $\log_{\mathbf{s}}\colon\mathbb{S}^n\to\mathcal{T}_{\mathbf{s}}\mathbb{S}^n$ the logarithmic map.
Then, by projecting the points in $\mathcal{S}$ onto the tangent $\mathcal{T}_{\mathbf{s}}\mathbb{S}^n$, we arrive at $$ \mathcal{S}^\prime=\{\log_{\mathbf{s}}(\mathbf{s}_i)\in\mathcal{T}_{\mathbf{s}}\mathbb{S}^n,i=1,\ldots,N\}. $$
Then, I'm thinking of calculating the sample mean and covariance of $\mathcal{S}^\prime$ and calculate the Mahalanobis distance on the tangent $\mathcal{T}_{\mathbf{s}}\mathbb{S}^n$, which if I understand correctly, is a Euclidean $n$-dimensional subspace of the ambient space $\mathbb{R}^{n+1}$.
I have the following questions:
- How can I express the points of $\mathcal{S}^\prime$ in a coordinate system of the tangent $\mathcal{T}_{\mathbf{s}}\mathbb{S}^n$ with the origin at $\mathbf{s}$? I understand that this seems like a trivial Differential Geometry question, but I'm a bit lost and I'd appreciate some guidance here.
- Is the standard basis of the ambient space a reasonable choice for working with the points on the tangent?
- What do you think in general about this idea? Would you think that that distance might capture the distribution of the points and give a "meaningful", "distribution-aware" distance?