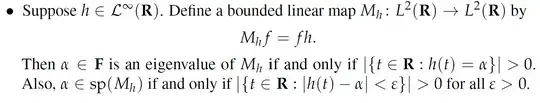Spectrum of the multiplication operator on $L^2(\mathbb R)$

Question

I am trying to verify an assertion in the second bullet point of Example 10.34 (Axler Measure Theory). Note that Axler uses the notation $\text{sp}(T)$ to denote the spectrum of $T$.

Let $E_\epsilon := \{t \in \mathbb R : | h(t) - \alpha | < \epsilon \}$.

Claim: $\alpha \in \text{sp}(M_h) \iff | E_\epsilon| > 0, \forall \epsilon > 0$

$(\Longrightarrow)$ Assume $\alpha \in \text{sp}(M_h)$.

This means that for each $f, g, \in L^2$, $$ (h - \alpha)f = M_h f - \alpha f = g $$ has no solution. In other words, $$ f = \frac g {(h - \alpha)} \notin L^2$$

The claim is satisfied if $\alpha \in e(M_h)$ because f is undefined on a set of positive measure (see the first proposition). So assume $\alpha \notin e(M_h)$. Then

$$ ||f|| = ||\frac g {(h - \alpha)}|| = \infty$$

And

\begin{align} \infty &= \left\Vert \frac g {(h - \alpha)} \right\Vert_2^2 \\ &= \left\Vert \frac {g^2} {(h - \alpha)^2} \right\Vert_1 \\ &\le \Vert g^2 \Vert_1 \left\Vert \frac 1 {(h- \alpha)^2} \right\Vert_\infty \\ &= \Vert g \Vert_2^2 \left\Vert \frac 1 {(h- \alpha)^2} \right\Vert_\infty \end{align}

The last equality implies that $$ \left\Vert \frac 1 {(h- \alpha)^2} \right\Vert_\infty = \infty $$

So we obtain $|E_\epsilon| > 0, \forall \epsilon > 0$.

$(\Leftarrow)$ Assume $|E_\epsilon| > 0, \forall \epsilon > 0$ holds for some $\alpha \in F$.

Suppose there exists $f, g \in L^2$ such that $f \neq 0$ and $$ f = \frac g {h - \alpha} $$

So $g \neq 0$. Define $$ E := \bigcup_{\epsilon > 0 } E_\epsilon $$ $$ F := \{ t \in E : g(t) \neq 0 \} $$

Because $f \in L^2$, we must have $ |F| = 0 $, otherwise the norm of $f$ is $\infty$. Now define $$ G := \{ t \in E^c : g(t) \neq 0 \} $$

Because $ g \neq 0$, we must have $|G| > 0$. Because $\mathbb R$ is $\sigma$-finite, we can assume that $G$ is finite (or otherwise intersect it with a finite measurable set, where that intersection will have nonzero measure).

Now let $H \subset E^c$ be such that $0 < |H| < \infty$.

So if $g = \chi_H$, don't we have a solution for $f$? On H, $\frac 1 {h - \alpha}$ can't be made arbitrarily large (because we're in $H$) or small (because its $ h - \alpha \in L^\infty$). So

$$ f = \frac {\chi_H} {h - \alpha} \in L^2 - {0}$$

What am I missing?

Answer 1

Presumably the underlying measure $m$ is Lebesgue's. The first part is the easiest: If $hf=\alpha f$ for some $f\in L_2\setminus\{0\}$ then $m(|f|>0)>0$ and on $\{|f|>0\}$, $h=\alpha$.Conversely, if $\mu(h=\alpha)>0$, then let $A\subset\{h=\alpha\}$ such that $0<m(A)<\infty$. Then $f=\mathbb{1}_A\in L_2(m)$ and $fh=\alpha f$.

As for the second part, here is a little lemma that will be useful:

Lemma A: Suppose $m$ is semi finite measure. If $h$ is a measurable function such that the operator $M_h:L_2\rightarrow L_2$ given by $g\mapsto gf$ is a bounded, then $h\in L_\infty$.

A proof of this can be found in this posting

We now prove the following:

Lemma B: The operator $M_hf =hf$ is bounded and onto iff $h\in L_\infty$ and there is $c>0$ such that $$c<|h|\leq\|h\|_\infty,\qquad m-\text{a. s.} $$ In either case, $M_h$ has a bounded inverse given by $M_{1/h}$.

Proof: (Sufficiency) If $0<c<|h|\leq\|h\|_\infty$ then $1/h\in L_\infty$. By Lemma A $M_{1/h}$ is bounded, and clearly $M_h$ is bijective with $M^{-1}_h=M_{1/h}$.

(Necessity): Suppose $h\in L_\infty$ is such that $M_h$ is onto.
Claim: $\mu(h=0)=0$. Otherwise, there would be a set $E$ of positive finite measure on which $h=0$. Then, the function $g=\mathbb{1}_E\in L_2$, $\|g\|_2>0$, but for no $f\in L_2$ is $M_{h}f=g$. This proves the claim.
Now, since $0<|h|$ $m$-a.s., it follows that $M_h$ is one-to-one, for $M_hf=M_hf'$ iff $hf=hf'$ $m$-a.s and so, iff $f=f'$ $m$-a.s. An application of the open map theorem (Theorem 5.10 in Rudin's Real and Complex Analysis for example) implies that $M_h$ has an inverse $M^{-1}_h:L_2\rightarrow L_2$, which is also a bounded operator. Notice that the inverse $M^{-1}_h$ is given by $f\mapsto f/h$, that is $M^{-1}_h$ is the product operator $M_{1/h}$. As $M_{1/h}$ is a bounded operator from $L_2$ into itself, by Lemma A $1/h\in L_\infty$. The conclusion follows by taking $c=1/\|h\|_\infty>0$

Finally, for $h\in L_\infty$, $\alpha\in\mathbb{C}$ is not in the spectrum of $M_h$ iff $M_{h-\alpha}:f\mapsto (h-\alpha)f$ is invertible. Then, by Lemma $B$, $\alpha$ is not in the spectrum of $M_h$ iff there is a constant $c_\alpha>0$ such that $$c_\alpha\leq|h-\alpha|\leq \|h-\alpha\|_\infty\qquad m-\text{a.s}$$ The conclusion in the OP follows.

Answer 2

It's easy to show that $L^\infty$ is a $C^*$-algebra, and $f\mapsto M_f$ is a faithful representation. Hence the spectrum of $M_f\in B(L^2)$ is the same as the spectrum of $f\in L^\infty$.

If necessary we may replace $f$ by $f-\alpha$, that is, we may assume $\alpha=0$. For any $\epsilon>0$, consider the function $$f_{\epsilon}=\begin{cases} 0 & \text{ if } |f(x)|<\epsilon \\ f(x) & \text{ otherwise} \end{cases}$$

By the given condition $E_{\epsilon}=\{x||f(x)|<\epsilon\}$ has positive measure, then $M_{f_\epsilon}$ has an eigenvector with eigenvalue $0$, hence $f_{\epsilon}$ is not invertible. And we have $\|f_{\epsilon}-f\|_{\infty}\le\epsilon$, therefore $f_{\epsilon}\rightarrow f$ as $\epsilon\rightarrow 0$. In any Banach algebra, the units form an open set, hence $f$ is not invertible either.

If there is $\epsilon>0$, such that $E_\epsilon$ has zero measure, then $\frac{1}{f}$ is defined almost everywhere,and $|\{x:|\frac{1}{f(x)}|> \frac{1}{\epsilon}\}|=|\{x: |f(x)|<\epsilon\}|=|E_{\epsilon}|=0$, hence $|\frac{1}{f}|_{\infty}\le \frac{1}{\epsilon}$, and $0$ is not in the spectrum of $f$.