2

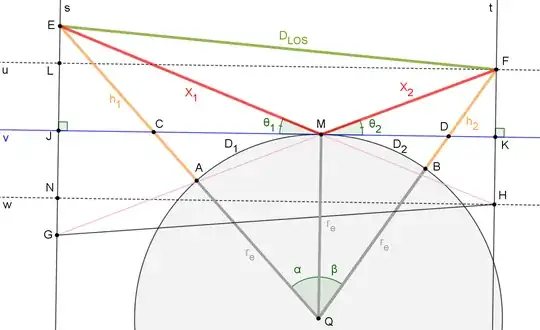
I am studying models for radio transmission where a signal can reflect on the ground before hitting the target. When modelling a flat earth, the geometry is pretty simple, and I can calculate the distances I need, but a spherical earth proves more difficult for me.

In the figure below, we know the earth radius $r_e$, we have antenna towers with known heights $h_1$ and $h_2$. We also know the distance between the towers along the surface of the earth from $A$ to $B$: $d=D_1+D_2$. There is a direct radio signal that goes as "line of sight" between the top of the towers from $E$ to $F$. There is also a signal that reflects on the planet surface at $M$. This means that the angles between the tangent $v$ of the planet at $M$ and the indirect path lines must be equal; $\theta_1=\theta_2$.

I need to know the central angles $\alpha$ and $\beta$, and the radio path lengths $D_{LOS}$, $X_1$, $X_2$ expressed in terms of $h_1$, $h_2$, $d$ and $r_e$.

When modelling a similar situation with a flat earth, I used a method of mirror images to get a nice looking solution. That's why I added the lines $MH$ and $GM$ to the figure, but I can't see how it helps in the spherical earth situation.

I have a hunch that there could be more than one solution. If that is the case, then maybe it is necessary to add these natural restrictions to make the solution unique: $r_e>h_1>h_2$.

Edit 1: Clarity.

spherical earth geometry

Jostein Trondal
  • 417
  • 3
  • 19
  • Nice and clear figure ! But what is exactly your question ? Deepening the analysis ? Finding alternate approaches ? A reference among others – Jean Marie Oct 26 '22 at 06:56
  • I need to know the central angles α and β, and the radio path lengths D_LOS, X_1, X_2 expressed in terms of h_1, h_2, d and r_e. – Jostein Trondal Oct 26 '22 at 06:57
  • You mean: be able to compute $\alpha$ and $\beta$ when you know the sum, say $\gamma:=\alpha + \beta$. Right ? – Jean Marie Oct 26 '22 at 07:05
  • As I understand now, $\angle AQP$, (that I called $\gamma$) is not given. What is given is distance $d=EF$ ; and $\gamma$ is obtained through formula: $d^2 = (r+h_1)^2+(r+h_2)^2-2 (r+h_1)(r+h_2) \cos(\angle AQP)$. Right ? (I use lower case d instead of D because D is already a point in your figure!) – Jean Marie Oct 26 '22 at 07:21
  • 2
    This is known as Alhazen's problem: https://math.stackexchange.com/questions/3961401/alhazens-problem-history/3963600#3963600 See also https://en.wikipedia.org/wiki/Alhazen%27s_problem – Intelligenti pauca Oct 26 '22 at 07:32
  • 1
    This paper could be of help: https://arxiv.org/pdf/2012.02170.pdf – Intelligenti pauca Oct 26 '22 at 07:40
  • 1
    Yes, I know α+β = 2asin(d/(2r_e)) – Jostein Trondal Oct 26 '22 at 08:23
  • 1
    @JeanMarie There is no P, think you mean B. The given distance d is the arc length from A to B. – Jostein Trondal Oct 26 '22 at 09:08
  • Here's an analytical solution: https://archive.org/details/100GreatProblemsOfElementaryMathematicsDoverHeinrichDrrie/page/n205/mode/2up – Intelligenti pauca Oct 26 '22 at 11:05

0 Answers0