What is the optimal angle to kick a ball in rugby game?

Question

What is the best angle to kick a ball toward the other team such that when two teams run at each other the teams will meet (when the kicking team tackles the team with the ball) at the distance furthest back from the ball kicker as possible?

The way I understand it is that you have to account for a trade-off from trying to kick the ball as far as possible and trying to keep the ball in the air for as long as possible giving the team more chance to run towards it before it lands.

I understand how you can prove the optimal angle to kick a ball as far as possible is 45 degrees. But with a question like this, you also would have to account for the team running at the other while the ball is in the air.

This is what I have done so far assuming the players running speed = 5m/s, initial kicking speed = 20m/s, gravity = 10m/s. Also, let the initial distance between the two teams = h.

Let A be the position of the kicking team and B be the position of the receiving team.

$A$ $=$ $h$ - running speed (time of ball in air + time of ball since landed) $A = h - 5(t_1+t_2)$

$B =$ ($h$ - distance the ball travels) + running speed(time of ball since landed) $B = h -$ distance $+$ $5(t_2)$

I figure I can find expressions for the distance the ball travels and the total time the ball spends in the air using the projectile motion equations. I was then planning to find $t_2$ by equating $A$ and $B$, since when the teams meet their positions will be the same.

From then my idea is to differentiate and find a minimum value for $A$ or $B$. Does this make sense? Am I on the right track?

Answer 1

I think you are kinda on the right track. Let us denote the kicking angle that we seek as $\alpha$, $t_1$ for the time in the air, $x_1$ for the horizontal distance the ball travels in the air and $t_2$ for the time both teams are running. A is intially zero and B is initally at $h$. When the ball lands A is at $5 t_1$ and team B is at $h$. Then they both run so in the end: $$ A=5(t_1+t_2) $$ $$ B=h-5 t_2. $$ Both of these quantities also need to be equal to $x_1$ for your requirement.

Equating A=B, you get $10t_2=h-5t_1$, or $t_2=\frac{h}{10}-\frac{t_1}2$. Substituting we find $\begin{equation}\label{eq:1} A=5t_1+\frac{h}2 -5\frac{t_1}2=5\frac{t_1}2+\frac{h}2. \end{equation}$

Without air resistance, the horizontal velocity of the ball is constant $v_x=v \cos(\alpha)=20 \cos(\alpha)$. Since the horizontal velocity is constant, it is equal to $\frac{x_1}{t_1}$, so $x_1=20 \cos(\alpha) t_1$.

The time in the air $t_1$ is found from $$0=y(t_1)=v_y t_1 - g \frac{t_1^2}2=20 \sin(\alpha) t_1-10 \frac{t_1^2}2. $$ Since $t_1\neq 0$, we have $$ t_1=4 \sin(\alpha). $$

Now we equate what we got for $A$ and $x_1$, $$ 20 \cos(\alpha) t_1 = 5\frac{t_1}2+\frac{h}2 $$ $$ 80 \cos(\alpha) \sin(\alpha) = 10 \sin(\alpha)+\frac{h}2. $$ $$ 160 \cos(\alpha) \sin(\alpha) - 20 \sin(\alpha)=h. $$

This equation can be solved for $\alpha$, for example setting $w=\tan(\frac{\alpha}2)$, we can rewrite it with the t-formulas as $$ w^4+360 h^{-1} w^3 +2 w^2-280 h^{-1} w +1. $$ This can be solved analytically ( https://en.wikipedia.org/wiki/Quartic_function#Ferrari's_solution ) but the exact solution is very long without the value of $h$.

Answer 2

So while your hands on approach may certainly be pushed to a correct answer I believe a more analytical and abstract approach may help to understand the problem better.

We will disregard air resistance for the sake of simplicity and we also note that we can disregard the length of the field $h$ since we are only interested in shooting into the opponent side of the field. If we shoot in our half of the field it is best to shoot exactly to $h/2$ and one can solve for the angle. Draw a coordinate system as depicted below:

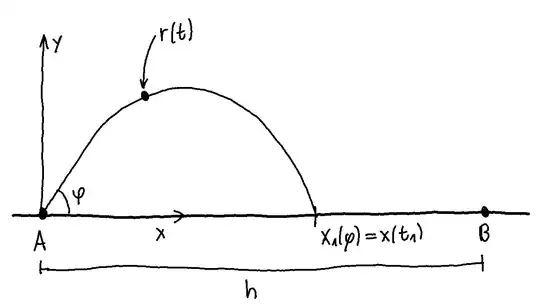
Let $r(t)=(x(t),y(t))$ denote the position of the ball at time $t$ with initial conditions $r(0)=(0,0)$ and $r'(0)=w(\cos(\varphi),\sin(\varphi))$, where $w$ is the speed at which the ball was kicked and $\varphi$ is the angle at which the ball was kicked. Also let $v$ be the speed at which the teams run at each other and let $x_1(\varphi)$ denote the the $x$-coordinate of the ball when it hits the ground at the hitting time $t_1$.

With Newton's laws we can deduce that $r(t)=r'(0)t+\frac{1}{2}(0,-g)t^2$ and hence we get the well known projectile trajectory $$ x(t)=w \cos(\varphi) t,\text{ } y(t)=w \sin(\varphi) t - \frac{1}{2}gt^2. $$ We would like to maximise $x_1(\varphi)$ under the restriction that the ball hits the ground and at the same time we would like to minimise the distance of our team to the ball when it hits the ground as far as I understand.

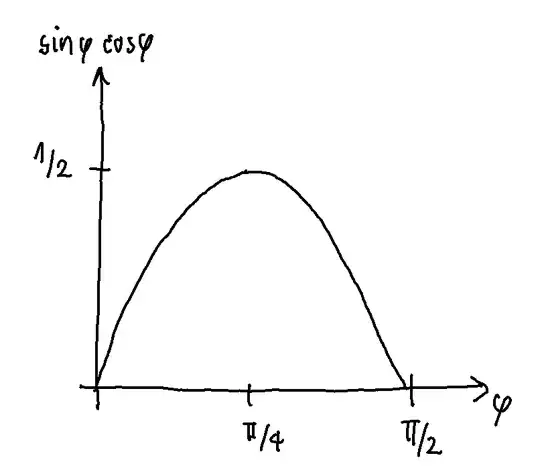
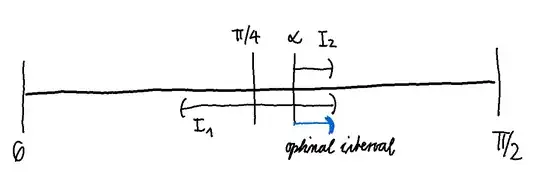
One can easily figure out that $x_1(\varphi)=2\sin(\varphi)\cos(\varphi)\frac{w^2}{g}$ (simply set $y(t)=0$ and plug it into $x(t)$) and hence scales like $x_1(\varphi)\sim \sin(\varphi)\cos(\varphi)$ and this function has one maximum at $\varphi = \frac{\pi}{4}$ which is the optimal angle to shoot the ball as far as possible. Hence we are interested in the interval $\varphi\in I_1=(\frac{\pi}{4}-\varepsilon;\frac{\pi}{4}+\varepsilon)$ for small $\varepsilon>0$.

On the other hand we would like be able to receive the ball when it lands, that is the distance between the ball when it landed to our team $d(\varphi)=vt_1-x_1(\varphi)$ should be $\geq 0$. Plugging in the formula above actually reduced the relevant data $\tilde{d}(\varphi)=|v-w\cos(\varphi)|$. This function achieves its minimum at $\varphi=\arccos(\frac{v}{w})$ and including the sign discussion we hence are interested in the interval $\varphi\in I_2=(\alpha;\alpha+\delta)$ for $\delta>0$ small and $\alpha=\arccos(\frac{v}{w})$.

Thus the optimal angles for the rugby ball problem must lie in the intersection of those two intervals $I_1\cap I_2$. Considering that the ball is faster than the players, i.e. $w>v$, we must have $\alpha>\frac{\pi}{4}$. if $\varphi>\alpha$ the team was able to pass the ball already and for $\varphi<\alpha$ the team is still behind the ball.

Conclusion

Plugging in your numbers gives an $\alpha$ which is far too big to actually get a good shot. One would need to run about $\frac{\sqrt 2}{2}$-times slower than shoot (or slightly less) to get a good $\alpha$ close to $\frac{\pi}{4}$. One could also vary the shooting speed $w$ but note that the hitting distance $x_1(\varphi)$ scales quadratically with the shooting speed $w$ and this would be another interesting problem to consider. But under the assumption of fixed shooting speed there is only the possibility to run faster or shoot in your half of the field to go safe. Either way in the realistic dimensions you've given the opponent team will be able to catch the ball first if you try to shoot it as far as possible with respect to shooting angle.