A Cycle of Simplex Method Has At Least Six Iterations

Question

I am studying the cycling of simplex method. In a 1969 paper A Note on Cycling in the Simplex Method by Marshall and Suurballe, the authors mentioned at the beginning of Section 6, page 136 that

Yudin and Gol'shtein showed in [4] that for the primal simplex method to cycle the problem must have $m\ge 2$, and for $m=2$ there must be at least six iterations of the algorithm.

Here [4] refers to the 1965 book Linear Programming by Yudin and Gol'shtein. However, I do not have access (online or offline) to this book. I wonder if someone could provide a proof of the fact mention above? Or does some other book contain a proof?

Answer 1

Pages 5 and 6 of "Cycling in linear programming problems" by Saul I. Gassa and Sasirekha Vinjamurib, and "A collection of cycling problems in linear programming" by Yaguang Yang, includes two models from that mentioned of by Yudin and Gol'shtein which should help assist you to prove that claim. Here are the models from both of those papers:

$$\max\quad x_3-x_4+x_5-x_6$$ Subject to, $$x_1+2x_3-3x_4-5x_5+6x_6=0$$ $$x_2+6x_3-5x_4-3x_5+2x_6=0$$ $$3x_3+x_4+2x_5+4x_6+x_7=1$$ $$x_j\ge0$$ Solution: $x_1=2.5, x_2=1.5, x_5=0.5$; Maximum = $0.5$; Cycle = $6$. $$\max\quad x_3-x_4+x_5-x_6$$ Subject to, $$x_1+x_3-2x_4-3x_5+4x_6=0$$ $$x_2+4x_3-3x_4-2x_5+x_6=0$$ $$x_3+x_4+x_5+x_6+x_7=1$$ $$x_j\ge0$$ Solution: $x_1=3, x_2=2, x_5=1$; Maximum = $1$; Cycle = $6$.

From:

Yudin DB, Gol’shtein EG. Linear programming. Israel Program of Scientic Translations, Jerusalem, 1965.

In either paper, there are more examples that depict this mentioned six iteration phenomena

---

The paper "Visualizing and Constructing Cycles in the Simplex Method" by David Avis, Bohdan Kaluzny and David Titley-Péloquin has an image snipit from Yudin and Gol'shtein's book that also shows these models:

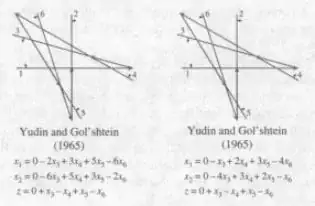
Model one from image: $$z = x_3-x_4+x_5-x_6$$ Subject to: $$x_1+2x_3-3x_4-5x_5+6x_6=0$$ $$x_2+6x_3-5x_4-3x_5+2x_6=0$$

Model two from image: $$z = x_3-x_4+x_5-x_6$$ Subject to, $$x_1+x_3-2x_4-3x_5+4x_6=0$$ $$x_2+4x_3-3x_4-2x_5+x_6=0$$

The only difference between the first models and these ones is the removal of one constraint. Playing around with these might give you the solution you are looking for.

---

After playing around with the above models, it became apparent that this is a special case where the authors Yudin and Gol'shtein assumed a closure state of the model has to happen where:

1. Simplex will terminate after a finite number of steps for reasons of unboundedness.
2. Simplex will be terminate after a finite number of steps upon arrival to a basic feasible solution.

This is more noticeable when this answer links a study sheet which confirms such a conversion took place, as in the above models the number of variables in the objective function equals four (pre-slack of $x_1$ and $x_2$), and the amount of constraints there are two, thus we satisfy $n-m=2\rightarrow 4-2=2$ for the proof, and in either model above, Simplex will terminate after six steps for the mentioned reasons.