Discuss the equation $\dot{x}=x^2-\frac{t^2}{1+t^2}$.
- Make a numerical analysis.
- Show that there is a unique solution which asymptotically approaches the line $x=1$.
- Show that all solutions below this solution approach the line $x=$ $-1 .$
- Show that all solutions above go to $\infty$ in finite time.
This is a problem of Teschl ODE qn 1.30
For the numerical analysis, we have the nullclines are $x_{+}=\frac{t}{\sqrt{\left(1+t^{2}\right)}}$ and $x_{-}=-\frac{t}{\sqrt{\left(1+t^{2}\right)}}$ which are supersolution and subsolution respectively which has given me 3 regions see the picture attached. We can focus on $t\geq 0$ part only.
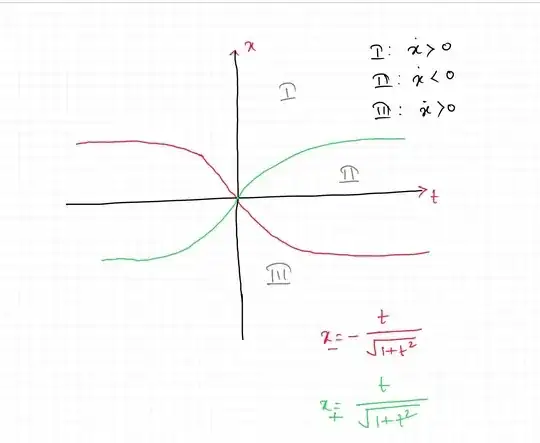
Now I can also see from xpp that the behaviour of the solution goes in the way
I am unable to make the proof rigorous. I know the theorem:
Let $x_{+}(t), x_{-}(t)$ be super, sub solutions of the differential equation $\dot{x}=f(t, x)$ on $\left[t_0, T\right)$, respectively. Then for every solution $x(t)$ on $\left[t_0, T\right)$ we have $$ x(t)<x_{+}(t), \quad t \in\left(t_0, T\right), \quad \text { whenever } \quad x\left(t_0\right) \leq x_{+}\left(t_0\right) $$ respectively $$ x_{-}(t)<x(t), \quad t \in\left(t_0, T\right), \quad \text { whenever } \quad x\left(t_0\right) \geq x_{-}\left(t_0\right) $$
but I am unable to find other good super and subsolutions to make it work. Let me know if I need any other theorems.
Also, my guess is that the one unique solution starts at an irrational initial point $\alpha$ which is in between $0.544592<\alpha<0.54453$. I got that while playing with xpp.
see this
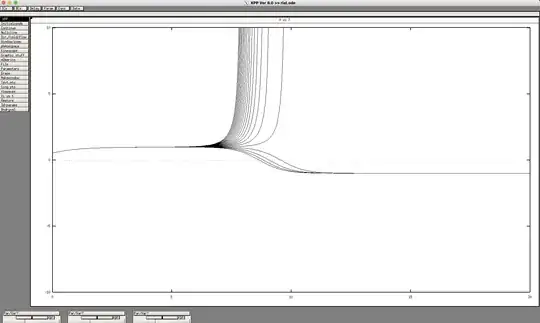More Information after trying:
So I am guessing that $x=-\sqrt{-c+\frac{t^{2}}{1+t^{2}}}$ is a super solution or not, where $c\in (0,1)$. If it is so then it will help me with part c of the problem. But the equation is getting cubic. If you are also trying in the same direction let me know.
