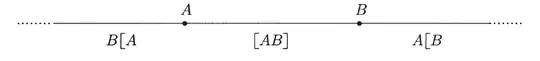1

My geometry book defines space abstractly as a non empty Set $\mathcal{R}$. To that the author adds a function $d \colon \mathcal{R} \times \mathcal{R} \to \mathbb{R}$. $d$ is supposed to represents an distance measure. Then it introduces three axioms, of which im only going to mention the first two because the author defines a straight line only using these two axioms

  • $d$ has all properties of a metric function.
  • For all two different points $A,B \in \mathcal{R}$ and for all $\delta >0$ there exists exactly one point $C \in \mathcal{R}$ such that $d(B,C) = \delta$ and $d(A,C) = d(A,B)+d(B,C)$.

Using these two axioms the author defines a line trhough $A$ and $B$ as $$\lbrace C \in \mathcal{R} \colon d(C,A)+d(A,B)=d(C,B) \rbrace \cup \lbrace C \colon d(A,C)+d(C,B)=d(A,B) \rbrace \cup\lbrace C \colon d(A,B)+d(B,C)=d(A,C) \rbrace. $$

enter image description here

$B[A$ is the first set, $[A,B]$ the second and $A[B$ the last set. The author draws this line here and the definition makes sense if you already know what a line is. But if we were to only view a line trhough the axioms, what is preventing us from also calling the following a "line" 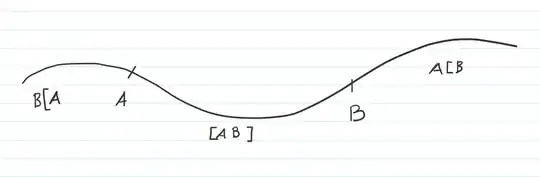enter image description here Non of the two axioms are necessarily violated as far as I can see. You could say let $\mathcal{R}$ be this curved line and given any metric $d$ both axioms are fulfilled. So what is a straight line?

Roger Crook
  • 371
  • 1
    Nothing. You can come up with an alternative model for the axioms but bear in mind that the axioms were created with a straight line in mind, not the other way around. – John Douma Sep 09 '22 at 17:01
  • 1
    You might be interested in this discussion of the flatness of a torus: https://math.stackexchange.com/questions/4377254/why-is-the-surface-of-a-torus-flat - the fact that a torus might even possibly be regarded as flat can be surprising. We can embed a one or two dimensional space in a space of higher dimension in various ways. – Mark Bennet Sep 09 '22 at 17:37
  • What do you mean by "given any metric $d$"? Of course you can define some metric according to which your wavy line fits the author's definition, but anyone can define a different metric according to which the straight line through $A$ and $B$ takes a different path. (That assumes we have a two-dimensional space.) – David K Sep 10 '22 at 00:36
  • It is always possible to take a particular mathematical model of your axioms (or any axioms) and to impose extra structure which is irrelevant to those axioms. – Lee Mosher Sep 10 '22 at 02:31
  • Depends what your definition of "straight" is. Have a look at the "geodesic equation" if you're interested. – K.defaoite Sep 11 '22 at 10:17

1 Answers1

1

You are showing a picture of a curvy line embedded in a planar image. There are many technically possible ways for what the metric could be here, but two are particularly plausible.

  1. You use the Euclidean metric of the containing plane.

    So distance between any two points is what you would measure with a ruler. In this setup triangle inequality will lead to the direct connection between any two points being shorter than if you first go to a point on the curve between them and then do the destination. Except if the three points happen to be on a straight line. So your wavy curve would not meet the conditions in your formulas, the equalities would in general not hold.

    This is the extrinsic view, of someone looking at the curve from the outside.

  2. You use the path length metric along the curve.

    In that case, you can't really “see” the surrounding plane in your formulas. You can only speak about distances between points on the curve. You are living on a one-dimensional string, and you don't have any indication that the string does not form a straight line. So for every point and purpose you can call this a straight line, and your definition allows you to do so.

    This is the intrinsic view, of someone living on the curve and not perceiving the surrounding plane.

You can come up with even more weird metrics, where you have distances for all the pairs of points in the plane, and still your wavy curve satisfies the conditions. For intuition imagine the curve as lying in some valley between really steep cliffs in 3D, so that the 3D distance would favour going through the valley and not over the hills, but you don't see the hills on the 2D top down projection.

Perhaps thinking in terms of “geodesics” rather than in terms of “straight lines” would be more suitable for making intuition and definition fit a bit better in this and similar situations. Although a geodesic is more like a line segment, and not the infinite line your formulas describe.

MvG
  • 44,006
  • I agree with your second point. The first one not so much. Lets say our abstract space $\mathcal{R}$ is a plane (i know we havent defined a plane yet but just imagine a sheet of paper). In order to introduce the euclidian norm we first need to embedd $\mathbb{R}$ in $\mathcal{R}$ (a bijective function) and then we need to embedd another $\mathbb{R}$ into $\mathcal{R}$ which is also linear independent. I know I'm throwing in words which we haven't even defined yet but the point is, in order to introduce the euclidian metric we already need to know what a Line in $\mathcal{R}$ is. – Roger Crook Sep 12 '22 at 09:53
  • If you construct $\mathcal R=\mathbb R^2$ algebraically, I don't think you need any knowledge of straight lines to get Euclidean metric going and prove its properties. It's only when you tie that with your intuition of a flat and straight sheet of paper that you may run into trouble. It's not surprising that modern axioms for Euclidean geometry tend to treat line as an undefined concept. – MvG Sep 12 '22 at 14:10