17

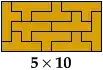
Some polyominoes are rectifiable, meaning they can tile some rectangle in the plane. For instance, the following tiling shows the $Y$-pentomino is rectifiable:

                                                                           enter image description here

On the other hand, some polyominoes (like the $S$-tetromino) are not, as should be obvious from trying a few configurations.

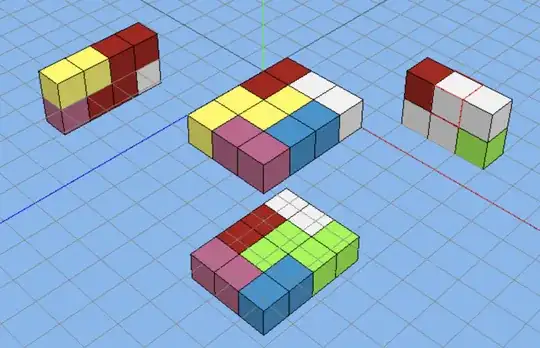
However, the $S$-tetromino does tile a $2\times 3\times 4$ box, if we consider the corresponding polycube. (Shown below is a sliced-open view of the tiling, with projections onto two of the faces shown off to the side.)

enter image description here

In fact, of the eight non-rectifiable pentominoes, I've found tilings for six of them:

  • The $R$ pentomino tiles a $5\times 6\times 6$ box.

  • The $S$ pentomino tiles a $2\times 4\times 5$ box.

  • The $T$ pentomino tiles a $3\times 10 \times 10$ box.

  • The $U$ pentomino tiles a $2\times3\times5$ box.

  • The $V$ pentomino tiles a $3\times5\times6$ box.

  • The $W$ pentomino tiles a $5\times6\times6$ box.

The $X$ pentomino obviously cannot tile any box, because it can never fit in the corner.

This leaves the $Z$ pentomino:

enter image description here

It's not apparent that it would find obstacles when trying to fit, but my computer-based search hasn't found any tilings of the shape within boxes of volume less than $360$. (Though given the minimum-volume boxes listed above, it's not clear this is all that strong evidence of impossibility.)

Questions about this problem:

  • Is there a known tiling or a known disproof?

  • Is there a coloring argument that restricts the possible dimensions beyond the trivial considerations (at least one side a multiple of $5$ and all dimensions at least $3$)?

  • Is there literature more generally on the problem of tiling boxes with polycubes, or pieces of the literature on rectifiable polyominoes that carry over?

  • If the $Z$ pentomino can't tile a three-dimensional box, can it tile one of a higher dimension?

RavenclawPrefect
  • 18,328

1 Answers1

10

On Torsten Sillke's site you can find results for all the pentacubes, including the Z-pentacube for which 6x6x25 and 6x10x10 solutions are known. They were found by Yoshiya Wolf Shindo in 1997.

The 6x10x10 solution has 4-fold rotational symmetry around one axis, and 2-fold around the other axes, so it consists of 8 copies of a single shape of approximately size 3x5x5 that fit together to form the block.

   51 52 52 36 38 30 30 21 15 15
   51 52 40 36 36 36 30 21 21 21
   52 52 53  z 33 36 30 30 14 21
   53 53 53  z  z  z  z  z 23 23
   53 55 55  z  z  z  z 22 23 11
   54 55 41  z  z  z  z 23 23 24
   55 55  z  z  z  z  z 24 24 24
   56 44 42 42 34 35  z 24 25 25
   56 56 56 42 34 34 34 29 25 12
   57 57 56 42 42 31 34 25 25 12

47 47 38 38 38 27 26 26 15 19
   51 47 40 40 40 28 28 19 19 19
   48 47 47  z 33 33 33 19 14 11
   48 43 41  z  z  z  z  z 14 11
   49 43 41  z  z  z  z 22 14 11
   54 44 41  z  z  z  z 22 13 17
   54 44  z  z  z  z  z 22 13 10
   54 44 50 35 35 35  z 20 20 10
   50 50 50 37 37 29 29 29 20 12
   50 57 39 39 32 31 31 31 20 20


45 45 38  o  o 27 26 15 15 16
   51 45  o  o 40 27 28 16 16 16
   51 45 45  z  o 27 33 16  o 11
   48 43 41  z  z  z  z  z  o  o
   49 49 49  z  z  z  z  o 14  o
    o 44  o  z  z  z  z 17 17 17
    o  o  z  z  z  z  z 22 13 10
   54  o 46 35 32  o  z 18 18 12
   46 46 46 37 32 29  o  o 18 12
   46 57 57 39 32  o  o 31 18 18


.  .  .  .  . 26 26  .  .  .
.  .  .  .  .  . 28 28  .  .
. 43  .  .  . 27  .  .  .  .



48 43  .  .  .  .  .  .  .  .
   48  . 49  .  .  .  .  .  .  .
    .  .  .  .  .  .  . 17  . 10
    .  .  .  .  .  .  .  . 13 10
    .  .  .  . 32  .  .  . 13  .
    .  . 37 37  .  .  .  .  .  .
    .  .  . 39 39  .  .  .  .  .
Jaap Scherphuis
  • 14,744