Integral of hyperbolic function combined with a polynomial over symmetric interval

Question

In a follow up computation to a previous question I stumbled across the following integral.

$$ \int_{-\infty}^\infty \frac{\text{sech}^3(z)}{\pi + 2 i z} \,dz \ .$$

First thing I did to solve it was to consider only the even part since the odd part will vanish over the given interval. This left me with

$$\int_{-\infty}^{\infty} \underbrace{\frac{\pi \text{sech}^3(z)}{\pi^2 + 4 z^2}}_{=:f(z)} \,dz \ .$$

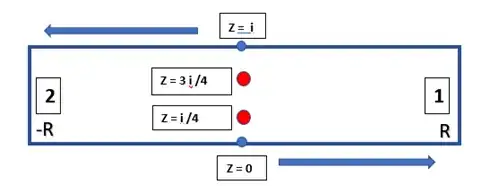
I tried to solve it using the methods of contour integration with the positively oriented simple closed contour $\gamma: \ $ $-R \to R \to R+ i \pi \to -R + i \pi \to -R$ ,encircling a pole of order 4 at $z = i \pi/2$. With the residue theorem, I got

$$ \oint_\gamma f(z) \,dz = 2 \pi i \ \text{Res}\left( f(z), z = \frac{i \pi}{2} \right) = \frac{2 + \pi^2}{4 \pi^2} \ .$$

Next, I evaluated the integrals along the "edges" (line segments) of $\gamma$. For reasons of simplicity, let's call them $$ \gamma_1: -R \leq z \leq R, z \in \mathbb{R} \ ,$$ $$ \gamma_2: R \leq z \leq R + i \pi, z \in \mathbb{C} \ ,$$ $$ \gamma_3: R + i \pi \leq z \leq -R + i \pi, z \in \mathbb{C} \quad \text{and}$$ $$ \gamma_4: -R + i \pi \leq z \leq -R, z \in \mathbb{C} \ .$$

The integral $\lim_{R\to \infty} \int_{\gamma_1} f(z) \,dz$ is the target integral. Using the subsequent changes of the integration variable given by $z \to t + i \pi$ and $t \to - z$ gives that

$$ \int_{\gamma_1} f(z) \,dz = \int_{\gamma_3} f(z) \,dz \ .$$

For the other two integrals I found with the change of variables $z \to R + i t$, $\,dz \to i \,dt$ and integration over the interval $[0,\pi]$ (for $\gamma_4$, I used an additional change $t \to - t$), that

$$ \left|\int_{\gamma_{2,4}} f(z) \,dz\right| = 0 \ .$$

To get there I used the Riemann integral inequality (Is there a proper name for this?) $|\int_a^b f(x) \,dx| \leq \int_a^b |f(x)| \,dx$, the expansion of $\text{sech}^3(z)$ in terms of exponential functions, the reversed triangle inequality $\frac{1}{|a-b|} \leq \frac{1}{||a|-|b||}$ and took the limit $\lim_{R\to \infty} f(z)$. I arrived at

$$\oint_\gamma f(z) \,dz = 2 \int_{\gamma_1} f(z) \,dz = \frac{2 + \pi^2}{4 \pi^2} $$

and thus

$$ \int_{-\infty}^{\infty} f(z) \,dz = \frac{2 + \pi^2}{8 \pi^2} \approx 0.15033 \ . $$

Unfortunately, this does not coincide with the numeric result (with interval for integration $-200 \leq z \leq 200$) where I get

$$ \int_{-\infty}^{\infty} f(z) \,dz \approx 0.437919 \ .$$

Can anyone help me find the mistake, I made? Thanks in advance :)

Answer 1

We can use a rectangular contour to solve the problem. It is convenient to consider the initial integral $$I=\int_{-\infty}^\infty \frac{\text{sech}^3(z)}{\pi + 2 i z} \,dz=\frac{1}{2}\int_{-\infty}^\infty\frac{1}{\cosh^3(2\pi t)}\frac{dt}{\frac{1}{4}+iz}=\frac{1}{2}\int_{-\infty}^\infty\frac{1}{\cosh^3(2\pi t)}\frac{dt}{\frac{1}{4}-iz}=\frac{1}{2}J_1\Big(\frac{1}{4}\Big)$$ Now we need to evaluate $$J_1(a)=\int_{-\infty}^\infty\frac{1}{\cosh^3(2\pi t)}\frac{dt}{a-it}=\frac{\partial}{\partial a}\int_{-\infty}^\infty\frac{\ln(a-it)}{\cosh^3(2\pi t)}dt=\frac{\partial}{\partial a}J_0(a)$$ To evaluate $J(a)$, we take into consideration that $$\ln(a-iz)=\ln\Gamma(a+1-iz)-\ln\Gamma(a-iz)=\ln\Gamma(a-i(z+i))-\ln\Gamma(a-iz)$$ and also that $\cosh(2\pi(z+i))=\cosh(2\pi z)$.

We can write $J_0(a)$ as a contour integral along a rectangular contour: $$J_0(a)=-\oint\frac{\ln\Gamma(a-iz)}{\cosh^3(2\pi z)}dz=-2\pi i\sum\operatorname{Res}\frac{\ln\Gamma(a-iz)}{\cosh^3(2\pi z)}$$

We have a couple of third-order poles inside the contour (at $z=\frac{i}{4}, \frac{3i}{4}$).

Taking, for instance, $z=\frac{i}{4}+\epsilon$ and decomposing the integrand: $$\frac{\ln\Gamma(a-iz)}{\cosh^3(2\pi z)}\bigg|_{z=\frac{i}{4}+\epsilon}=i\frac{\ln\Gamma\big(a+\frac{1}{4}\big)-i\epsilon\psi\big(a+\frac{1}{4}\big)-\frac{\epsilon^2}{2}\psi^{(1)}\big(a+\frac{1}{4}\big)+O(\epsilon^3)}{(2\pi\epsilon)^3\Big(1+\frac{(2\pi\epsilon)^2}{6}+O(\epsilon^4)\Big)^3}$$ The residue evaluation is straightforward: $$-2\pi i\underset{z=\frac{i}{4}}{\operatorname{Res}}\frac{\ln\Gamma(a-iz)}{\cosh^3(2\pi z)}=-\frac{1}{(2\pi)^2}\Big(\frac{1}{2}\psi^{(1)}\big(a+\frac{1}{4}\big)+\frac{(2\pi)^2}{2}\ln\Gamma\big(a+\frac{1}{4}\big)\Big)$$ In the similar way we find $$-2\pi i\underset{z=\frac{3i}{4}}{\operatorname{Res}}\frac{\ln\Gamma(a-iz)}{\cosh^3(2\pi z)}=\frac{1}{(2\pi)^2}\Big(\frac{1}{2}\psi^{(1)}\big(a+\frac{3}{4}\big)+\frac{(2\pi)^2}{2}\ln\Gamma\big(a+\frac{3}{4}\big)\Big)$$ and $$J_0(a)=\frac{1}{8\pi^2}\Big(\psi^{(1)}\big(a+\frac{3}{4}\big)-\psi^{(1)}\big(a+\frac{1}{4}\big)\Big)+\frac{1}{2}\Big(\ln\Gamma\big(a+\frac{3}{4}\big)-\ln\Gamma\big(a+\frac{1}{4}\big)\Big)$$ Therefore, $$J_1(a)=\frac{d}{da}J_0(a)=\frac{1}{8\pi^2}\Big(\psi^{(2)}\big(a+\frac{3}{4}\big)-\psi^{(2)}\big(a+\frac{1}{4}\big)\Big)+\frac{1}{2}\Big(\psi\big(a+\frac{3}{4}\big)-\psi\big(a+\frac{1}{4}\big)\Big)$$ $$I=\frac{1}{2}J_1\big(\frac{1}{4}\big)=\frac{1}{16\pi^2}\Big(\psi^{(2)}(1)-\psi^{(2)}\big(\frac{1}{2}\big)\Big)+\frac{1}{4}\Big(\psi(1)-\psi\big(\frac{1}{2}\big)\Big)$$ Taking $\psi(1)-\psi\big(\frac{1}{2}\big)= 2\ln 2, \,\psi^{(2)}(1)=-2\zeta(3)$ and $\psi^{(2)}\big(\frac{1}{2}\big)=-16\zeta(3)\big(1-\frac{1}{2^3}\big)=-14\zeta(3)$,

we get the answer: $$\boxed{\,\,I=\frac{\ln2}{2}+\frac{3}{4}\frac{\zeta(3)}{\pi^2}=0.437918...\,\,}$$