0

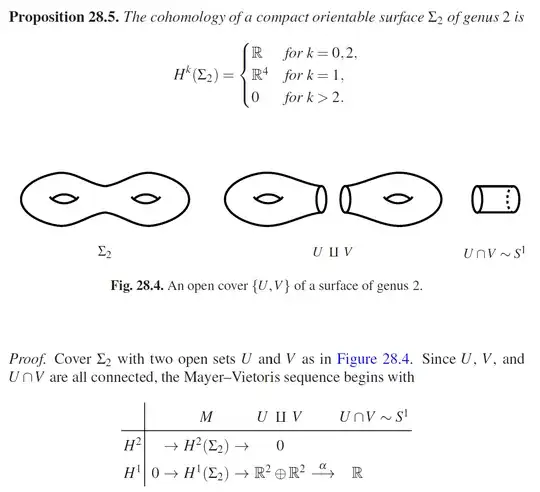
I'm confused by one part of Proposition 28.5 (Introduction to Manifolds, 2), which provides the cohomology of the genus 2 surface.

enter image description here

  1. What exact are the open sets $U$ and $V$? I thought they were tori, because the chart shows that $ H^1(U) \oplus H^1(V) \cong \mathbb{R}^2 \oplus \mathbb{R}^2 $. But then it has $H^2(U) \oplus H^2(V) = 0$, while $H^2(T^2) = \mathbb R$.

  2. In general, what is the cohomology of a torus with a side chopped off (like in Fig 28.4 below) is?

  3. Relatedly, is it generally the case that $H^k(U \sqcup V) = H^k(U) \oplus H^k(V)? $ In the former, we've cut out the intersection, so I don't see how it would have the same cohomology as the latter.

IsaacR24
  • 725
  • 5
  • 14
  • They are exactly drawn in the diagram; they're punctured tori. 2. Show that the punctured torus deformation retracts onto a wedge of two circles. 3. Yes.
    • – Qiaochu Yuan Aug 05 '22 at 17:58
  • I'm confused by your response to (2). $U$ appears to be something like $\Sigma_2 - \overline{B}$, where $\overline{B}$ is a closed ball in $\Sigma_2$ that effectively cuts it in half. Where is the puncture? I know that a point is homotopic to a open ball in $\mathbb{R}^n$, but I still don't follow your reasoning. – IsaacR24 Aug 05 '22 at 18:18
  • Sorry, I'm being a little sloppy. They are tori with discs cut out, which are homotopy equivalent to and hence have the same cohomology as punctured tori. – Qiaochu Yuan Aug 05 '22 at 18:20
  • Isn't your claim that $T^2 - D \simeq T^2 - {p}$ contradicted by this post? In particular, ${p} \ncong D$, and both are plane continua. – IsaacR24 Aug 06 '22 at 18:28
  • Here's the theorem I'm referring to: Two plane continua have the same shape if and only if their complements in $\mathbb{R}^2$ are homeomorphic. – IsaacR24 Aug 06 '22 at 18:29
  • There are two distinct issues with the argument you're trying to make here. 1) $T^2$ is not the plane. 2) A point and a disc have the same shape. – Qiaochu Yuan Aug 06 '22 at 18:32
  • Did you mean an open disc? Yes I understand that a point and open disc have the same shape. But a torus with open disc removed isn't open. – IsaacR24 Aug 06 '22 at 22:57