I shall expand on the hints I provided in the comments. First note that any symmetry of the icosahedron preserves distances, and so if the pair of vertices $\{u,v\}$ get transformed into $$g\star\{u,v\}=\{g\star u,g\star v\}=:\{u',v'\},$$ then $d(u,v)=d(u',v')$.
Suppose therefore that we have a partition $X=X_1\sqcup\cdots\sqcup X_k$ such that $G$ acts transitively on each $X_i$. Then the observation above implies that if $\{u,v\},\{u',v'\}\in X_i$ for some $i$, then $d(u,v)=d(u',v')$. I claim that taking exactly the partition of $X$ coming from $d$ is sufficient.
In order to prove this, let $X_i=\{\{u,v\}\mid d(u,v)=c\}$ for some fixed $c$. Let $\{u,v\},\{u',v'\}\in X_i$. Now, a key observation is that while $G$ may not act transitively on $X$, it does act transitively on the set of vertices of the dodecahedron. Therefore we can find $g\in G$ such that $g\star u'=u$.
If we define $w=g\star v'$ then we can reduce to the case we have $\{u,v\},\{u,w\}\in X_i$, and want to show that there is $h\in G$ such that $h\star\{u,v\}=\{u,w\}$. Such an $h$ must lie in the stabiliser of $u$, $\textrm{Stab}_G(u)$. By considering a picture of an icosahedron, t is easy to convince yourself (by putting $u$ at the top say), then $\textrm{Stab}_G(u)$ acts transitively on the set of all vertices a fixed distance from $u$.
Thus, the required $h$ exists, and the element $gh$ maps $\{u,v\}\mapsto\{u,w\}$ as required.
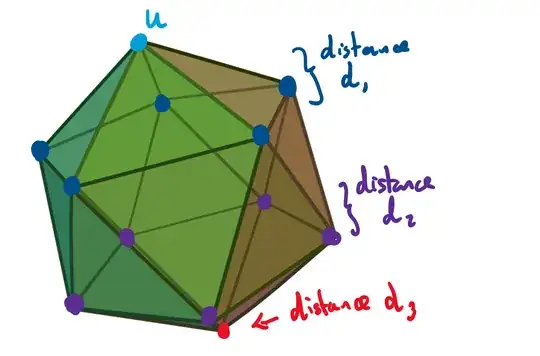
(Image by DTR (CC BY-SA 3.0))
This picture also shows that there are three possible distances for a pair of points to be apart, which I'm calling $d_1, d_2,d_3$. Let $X_1, X_2,X_3$ be the corresponding sets.
Finally we must compute the cardinalities of these sets. $|X_1|$ is the number of edges in the icosahedon, ie $\frac{20\times 3}{2}=30$. $|X_3|$ is the number of antipodal vertices, ie $\frac{20\times 3}{5\times 2}=6$. This leaves $|X_2|=|X|-|X_1|-|X_3|=30$.
