Find area of the largest possible equilateral triangle inscribed in a isosceles triangle

Question

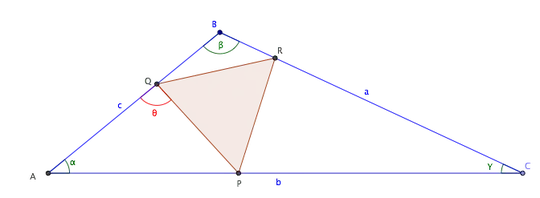
What is the area of the largest equilateral triangle that can be inscribed in an isosceles triangle?

There is a similar question asked before that might be helpful:

The main problem with this is that sometimes is it unusable. I tried it and it doesn't work.

So here is what I find out from playing around with GeoGebra $$ l_\max = \frac{3\sin\alpha}{\sin(2\alpha-60^\circ)}. $$

The formula seems to only work if two of the angles are equal or greater than $60^\circ$.

But if we use it with a triangle where two of the angles are less than $60^\circ$, it just doesn't work. Can someone explain why?

1. Why the formula can't be applied to a triangle that two of the angle are less than $60^\circ$?

2. If so is there any general formula for this?

Answer 1

Let's name vertices, sides and angles of the triangle as in figure below, with $c\le a\le b$ and consequently $\gamma\le \alpha\le \beta$. Let then $PQR$ be the inscribed equilateral triangle, with $P\in AC$, $Q\in AB$ and $\theta=\angle AQP$. Applying the sine rule to triangles $APQ$, $BQR$, it is not difficult to find the side $l=PQ$ as a function of $\theta$: $$ l={c\sin\alpha\sin\beta\over \sin\alpha\sin(60°+\theta-\beta) +\sin\beta\sin(\alpha+\theta)}. $$

As in the isosceles case, $dl/d\theta=0$ when $l$ reaches its minimum value. The maximum is reached for a limiting value of $\theta$. There are two cases to discuss.

1. If $\alpha>60°$, the limiting values of $\theta$ are reached when $Q=B$ (that is $\theta =\beta-60°$) or $Q=A$ (that is $\theta =180°-\alpha$), corresponding to the values of $l$: $$ l_1={c\sin\alpha\over\sin(\alpha+\beta-60°)}, \quad l_2={c\sin\beta\over\sin(\alpha+\beta-60°)}. $$ In this case $l_2>l_1$, hence the maximum of $l$ is given by $l_2$.

2. If $\alpha\le60°$, the limiting values of $\theta$ are reached when $Q=B$ (that is $\theta=\beta-60°$) or $R=B$ (that is $\theta =120°$). The first value corresponds to $l_1$ as written above, while the second value gives $$ l_2'={c\sin\alpha\over\cos(\alpha-30°)}. $$ In this case the maximum of $l$ is the greater between $l_1$ and $l_2'$.