Consider cubic splines $s( x, y )$ which interpolate values $y = \{ y_0, y_1, \dots,y_n \}$,
on the uniform grid $\{ 0, 1,\dots, n \}$.
Fix $s''(0) = s''(n) = 0$ (natural splines).
How big can
$$\operatorname{overshoot}( s; y ) \equiv \max_{0\le x\le n} s( x; y ) $$
be, over all splines $s( x; y )$ and all $0 \le y_i\le 1$?
Interpolating a pulse $[ 0\, 0\, 1\, 1\, 0\, 0 ]$ with Catmull-Rom splines overshoots to $\frac98$;
in $d$ dimensions, a "mesa" $[ 0\, 0\, 1\, 1\, 0\, 0 ]^d$ will overshoot to $({9 \over 8})^d$.
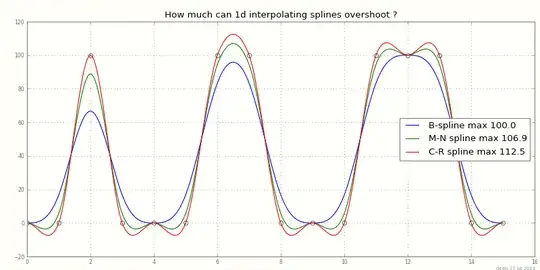
Can anyone point me to an upper bound for overshoot of tensor-product cubic splines on grids of integers in $d$ dimensions ? Or for quadratic splines ?
(Note that overshoot() is here defined as a max over $0 \le y_i\le 1$, half that over $-1 \le y_i \le 1$.)
Interpolating splines can be local or global. (Local C-R splines look at $4^d$ nearest neighbors of each $x$; IIR splines, described in Unser with IIR filters and implemented in scipy.ndimage, have infinite support.) With scipy's global IIR splines I see about twice the overshoot of local C-R:

References:
M. Unser, Splines: A perfect fit for signal and image processing ,
1999, 17p .
scipy.ndimage interpolation .
Wikipedia Bicubic interpolation
mentions overshoot, haloing, and ringing artifacts in 2d images.