2

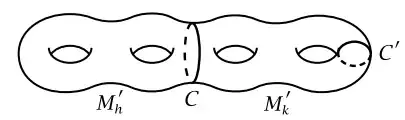
Let $M_g$ be a orientable surface of genus $g$, and let $C$ be a circle that separates $M_g$ into two compact subsurfaces $M_h'$ and $M_k'$ obtained from the closed surfaces $M_h$ and $M_k$ by deleting an open disk from each. Show that $M_h'$ does not retract onto its boundary circle $C$, and hence $M_g$ does not retract onto $C$. enter image description here

Suppose such a retraction $r:M_h' \to C$ exists, then $r \circ \iota=id$ and we have the induced maps $r_* : \pi_1(M_h') \to \pi_1(C), \iota_*: \pi_1(C) \to \pi_1(M_h')$ for which $$r_* \circ \iota_* = id_*$$

Now since $M_h'$ can be thought of as the $4h$-gon with the central disc removed we see that $C$ is homotopic to the loop $a_1b_1 \dots a_h^{-1}b_h^{-1}$ and thus sends a generator of $\pi_1(C)$ to $[a_1b_1 \dots a_h^{-1}b_h^{-1}]$. Now as $\pi_1(C) \cong \Bbb Z$ is abelian abelianizing we have that $$\iota_*^{ab} : \pi_1(C) \to \pi_1(M_h')^{ab}$$ sends a generator of $\pi_1(C)$ to $1$ and thus $\iota_*^{ab}$ is a trivial map.

However it's also injective as the functor $^{ab}$ gives that $(r_* \circ \iota_*)^{ab} = r_*^{ab} \circ \iota_*^{ab} = id_*^{ab}$ i.e. $\iota_*^{ab}$ has a left inverse. This is a contradiction since the trivial map cannot be injective.

I have few questions about this proof

  1. Is it a true statement that since $C$ is homotopic to $a_1b_1 \dots a_h^{-1}b_h^{-1}$ it sends a generator to $[a_1b_1 \dots a_h^{-1}b_h^{-1}]$?
  2. Can I conclude that $\iota_*^{ab}$ sends a generator to the identity under the abelianization as I do here?
hbghlyj
  • 5,361
Emil Grönberg
  • 297

1 Answers1

1

The answer is yes to both questions. For the first question this follows straight from the definition of $\iota_\ast$.

Notationally it is useful to write $[a,b]=aba^{-1}b^{-1}$ for the commutator of $a$ and $b$. Then the boundary $C$ represents the element which can be written as a product of commutators $$[a_1,b_1]\cdots[a_h,b_h].$$ Now, the abelianisation of a group is equal to the quotient of that group by its commutator subgroup. Since $C$ represents a product of commutators, this dies in the abelianisation. This proves that the answer to 2 is yes.

David Sheard
  • 2,537