Series of almost-alternating reciprocals of squares is non-zero

Question

Let $0<a<b<2$ be fixed, and consider the series \begin{equation} S:=\sum_{k=1}^\infty \frac{\big(\cos(k\pi a)-\cos(k\pi b)\big)}{k^2}. \end{equation} This series can readily be seen to be convergent. But for which values of $a$ and $b$, can we ensure that $S\neq 0$?

Answer 1

Let $$f(x)=\sum_{k=1}^{+\infty}\frac{\cos(k\pi x)}{k^2}$$ Then $$S=f(a)-f(b)$$ Thus your question is equivalent to determining the domains on which $f$ is injective.

First, $f$ is $2$-periodic, so if $b-a=2 n$ for $n\in\mathbb N$, then $f(a)=f(b)$.

Therefore, let's focus on $[0, 2)$.

Using the definition of the polylogarithm $$\text{Li}_n(z)=\sum_{k=1}^{+\infty}\frac{z^k}{k^n}$$ you can check that $$f(x)=\frac{\text{Li}_2(e^{i\pi x})+\text{Li}_2(e^{-i\pi x})}{2}$$ Then $$\begin{split} f^\prime(x)&=i\pi\frac{e^{i\pi x}\,\text{Li}^\prime_2(e^{i\pi x})-e^{-i\pi x}\,\text{Li}^\prime_2(e^{-i\pi x})}{2}\\ &=\frac{i\pi}{2}\left(\text{Li}_1(e^{i\pi x})-\text{Li}_1(e^{-i\pi x}) \right)\\ &=\frac{i\pi}2 \left(-\ln(1-e^{i\pi x}) + \ln(1-e^{-i\pi x}) \right)\\ &=\frac{i\pi}2\ln\left(-e^{-i\pi x}\right)\\ &=\frac{\pi^2}{2}(x-1) \end{split}$$ Thus $f$ decreases on $[0, 1)$ and increases on $[1, 2)$.

You can also directly integrate the derivative, to get $$f(x)=\frac{\pi^2}{6}+\frac{\pi^2}2\left(\frac {x^2} 2-x\right)=\frac{\pi^2}{4}(x-1)^2-\frac{\pi^2}{12}$$ Here's a plot of the function 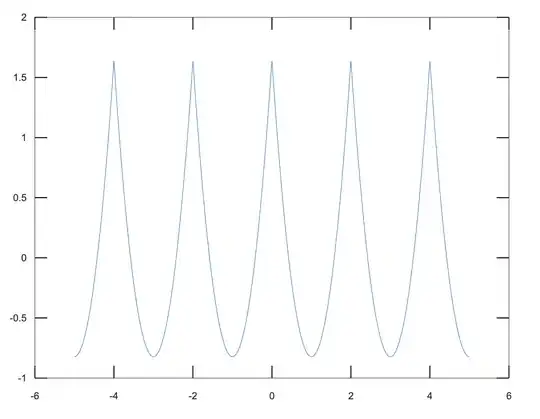As noted by @Greg Martin, the function is symmetric around $x=1$ (parabola). At this point you should have all the information you need to answer your question.

Answer 2

Use this result:

\begin{align} F(x) - F(0) &= \int_{0}^{x} \left(-\sum_{n=1}^{\infty} \frac{\sin (n t)}{n}\right)\, dt \\ &= \Im \int_{0}^{x} \left(-\sum_{n=1}^{\infty} \frac{e^{i n t}}{n} \right) \, dt \\ &=\Im \int_{0}^{x} \ln(1-e^{i t}) \, dt \\ &= \Im \int_{0}^{x} \ln \left(2\sin\left(\frac{t}{2}\right)e^{i(t-\pi)/2}\right) \, dt \\ &=\Im \int_{0}^{x} \left[ \ln \left(2\sin\left(\frac{t}{2}\right)\right)+\frac{i(t-\pi)}{2}\right]\, dt \\ &= \int_{0}^{x} \frac{t-\pi}{2} \, dt = \frac{x^2}{4}-\frac{\pi x}{2}\end{align} Since $F(0)=\frac{\pi^2}{6}$, this implies that $$\boxed{\sum_{n=1}^{\infty} \frac{\cos (n x)}{n^2} = \frac{x^2}{4}-\frac{\pi x}{2}+\frac{\pi^2}{6}}$$

Now, let $x=a\pi$ and $x=b\pi$

$$\begin{align} S&=\sum_{k=1}^{\infty} \frac{\cos (k\pi a)}{k^2}-\sum_{k=1}^{\infty} \frac{\cos (k\pi b)}{k^2}\\ \\ S&= \left(\frac{a^2\pi^2}{4}-\frac{a\pi^2}{2}+\frac{\pi^2}{6}\right)-\left(\frac{b^2\pi^2}{4}-\frac{b\pi^2}{2}+\frac{\pi^2}{6}\right)\\ \\ S&=0~~\Longleftrightarrow ~~a=b ~~~\text{or}~~~ a+b=2 \end{align}$$

So as long as $a\neq b$ and $a+b\neq 2$, then $S\neq 0$