An evaluation of $\int_{-\infty}^\infty \int_{-\infty}^\infty \ln\left(\frac{\text{sech}(x+yi)}{x+yi}-1\right)dxdy$

Question

Interested by What is $\int_0^\infty \ln \left(1-\frac{\sin x}{x} \right) dx $?, so the following integral may have an interesting evaluation:

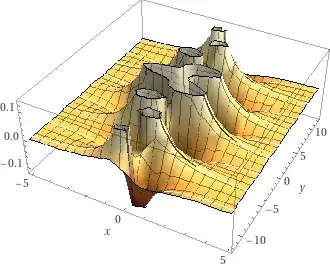
$$\text{Re}\int_{\Bbb C}\ln\left(\frac{\text{sech}(z)}z-1\right)dz$$ Here is a graph of the integrand. Notice the many vertical and horizontal asymptotes:

Here are some alternate forms: $$\text{Re}\int_\Bbb C\ln\left(\frac{\text{sech}(z)}z-1\right)dz =2 \text{Re}\int_0^\infty \int_{-\infty}^\infty \ln\left(\frac{\text{sech}(x+yi)}{x+yi}-1\right) dxdy =2 \text{Re}\int_{-\infty}^\infty \int_0^\infty \ln\left(\frac{\text{sech}(x+yi)}{x+yi}-1\right) dy dx= 2 \text{Re}\int_0^\infty \int_{-\infty}^\infty \ln(1-(x+y i)\cosh(x+yi)) -\ln((x+yi)\cosh(x+yi))dxdy$$ Although there is a closed form for the indefinite integral, the following one diverges: $$\int_0^\infty\int_{-\infty}^\infty\ln((x+yi)\cosh(x+yi))dxdy$$ Let’s expand the integrand. Since the integration bounds are the entire complex plane, we expand $\text{Re}\ln(x-1)$ with $A=\left\{x,y:\left|\text{Re}\left(\frac{\text{sech}(x+yi)}{x+yi}\right)\right|<1\right\}$, shown here, and $B=\Bbb C-A= \left\{x,y:\left|\text{Re}\left(\frac{\text{sech}(x+yi)}{x+yi}\right)\right|>1\right\}$, shown here

$$2 \text{Re}\int_0^\infty \int_{-\infty}^\infty \ln\left(\frac{\text{sech}(x+yi)}{x+yi}-1\right) dxdy=\text{Re}\iint_B \ln(\text{sech}(x+yi))-\ln(x+yi)-\sum_{n=1}^\infty \frac{(x+yi)^n(e^{2(x+yi)}+1)^n}{2^n e^{n(x+yi)} n} dxdy -2\text{Re} \iint_A\sum_{n=1}^\infty \frac{2^n e^{n(x+yi)}}{n(x+yi)^n(e^{2(x+yi)}+1)^n}dxdy $$

The next step is to expand each $\left(e^{2(x+yi)}+1\right)^n$ with a binomial series, but the integral is very messy at this step, with possible divergence. Surely we can’t do $\int_\Bbb C f(z)dz$ and have a single integral over the entire complex plane. Based on the “conjectures”, the integral may be a rational multiple of $\pi$:

What is $\displaystyle \int_{-\infty}^\infty \int_{-\infty}^\infty \ln\left(\frac{\text{sech}(x+yi)}{x+yi}-1\right)dxdy$?

Answer 1

Here's a partial result that's far too long for a comment. Let $a_n$ be the zeroes of $1 - z \cosh z$, indexed so that $a_0$ is the sole real zero and $a_{\pm n}$ is the zero near $\mathrm{Im}[z] = \pm(n-1/2)\pi$. Similarly, let $b_n$ be the zeroes of $z\cosh z$, indexed so $b_0 = 0$ and $b_{\pm n} = \pm i(n-1/2)\pi$. Then we (probably) have $$ \frac{\operatorname{sech} z}{z} -1 = \frac{1 - z \cosh z}{z \cosh z} = \prod_{n=-\infty}^\infty \frac{z-a_n}{z-b_n}. $$ The idea here is expressing the numerator and denominator as a Weierstrass product. However, I'm having trouble proving the normalization also works out to the above, though it does agree quite well with numeric evaluations. At any rate, assuming that that's true and everything converges the way I want it to, we have \begin{multline} \operatorname{Re}\left[\int_{\Bbb C}\ln\left(\frac{\text{sech}(z)}z-1\right)dz\right] = \sum_{n=-\infty}^\infty \operatorname{Re}\left[\int_{\Bbb C}\ln\left(\frac{z-a_n}{z-b_n}\right)dz\right] \\= \frac{\pi}{2}\sum_{n=-\infty}^\infty (|a_n|^2-|b_n|^2) = \pi\left(\frac{a_0^2}{2} + \sum_{n=1}^\infty \left[|a_n|^2 - \left(n-\frac{1}{2}\right)^2\pi^2\right]\right). \end{multline}

The terms of the sum go as $O([(n-1/2)\pi]^{-2})$, so it does converge. Unfortunately it doesn't do so very quickly, but numerically evaluating it anyways gives the integral as $4.10639338\approx 1.30710561\pi$. Might see if I can do better later, but this is something.