3

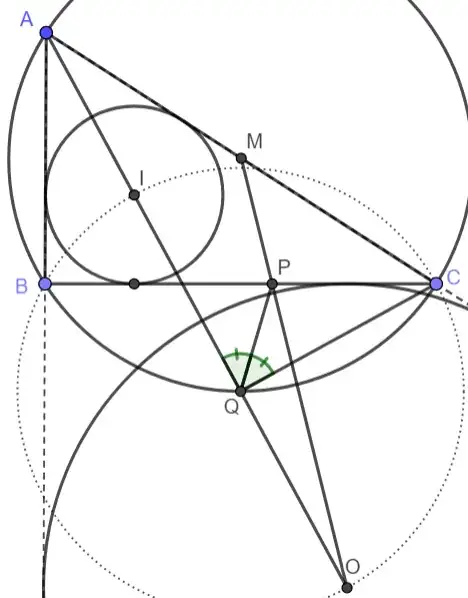
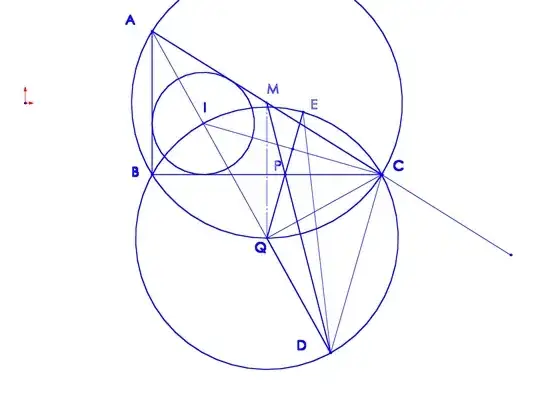
Given a triangle $\triangle ABC$ whose incenter is $I$, its $A-$exincenter is $O$, the midpoint of $AC$ is $M$, $P = OM \cap BC$ and $Q = AI \cap (ABC) \neq A$. Prove that $\angle AQP = \angle PQC$.

enter image description here

It is easy to see that $QB= QC=QO = QI$, so I thought about the spiral similarity between $AC$ and $IO$, but it is a weird one because its centers would be either points $C$ or $A$? Anyways, I couldn't find a simple solution neither find some harmonic pencil.

the great problem seems to be that point $M$

nonuser
  • 91,557
hellofriends
  • 2,048

2 Answers2

1

Let $IP$ meet $AC$ at $X$ and let $AO$ cuts $BC$ at $A'$.

Then we have \begin{align} (A,C;X,M)&= (PA,PC;PX,PM) \\ &= (PA, PA'; PI, PO) \\ &= (A,A'; I,O) \\ &=-1 \end{align}

Since $M$ is the midpoint of $AC$ it means $X=\infty$, so $IP||AC$.

But now it is easy to see that $BQPI$ ic cyclic and by simle angle chase we get the conclusion.

nonuser
  • 91,557
0

enter image description here

Hint: In figure CI and CD are interior and exterior bisectors of angle $ACB$. In triangle ICD, QE is perpendicular bisector of IC and it meets the bisector of angle QDC at E. In this way :

$\angle IQE=\angle EQC$

Now all you have to do is to show that P is on QE.

Hope it helps.

sirous
  • 12,694