0

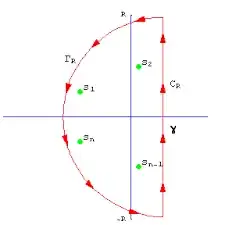
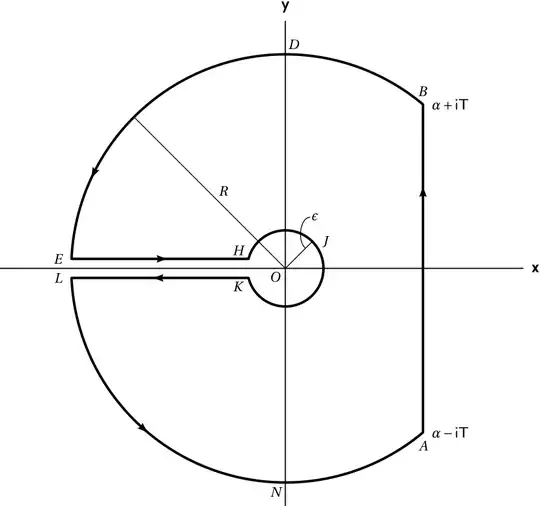
I was reading this question (Inverse Laplace Transform of $1/(s+1)$ without table) and read the following:

The pole is on the left half plane, so: $$\gamma(t)=\frac{1}{2i\pi}\int ^{i\infty}_{-i\infty}\frac {e^{st}}{s+1}\,\mathrm{d}s$$

  • What exactly is a "pole" of a function? Based on this other question I was reading (Finding poles, indicating their order and then computing their residues), it seems that the "pole" of a function is at all points where you are forced to divide by 0. Is this correct?

  • Once you have determined the "pole" of a function - how do you determine that the "pole" of the function 1/(s+1) is on the left half of the plane? Is this done by determining if the "pole" of this function has a "complex part"? (e.g. a + ib)

Thank you!

Note: I am asking this question with regards to calculating Inverse Laplace Transforms. For many common mathematical functions, I am guessing that the "poles" of these functions will be in the "left plane" - and thus, the "Gamma" term in the Inverse Laplace Transform will end up being 0 and thus facilitate the computation of the integral required in the Inverse Laplace Transform. Is this correct?

FShrike
  • 46,840
  • 3
  • 35
  • 94
stats_noob
  • 4,107
  • 3
    https://en.wikipedia.org/wiki/Zeros_and_poles, https://encyclopediaofmath.org/wiki/Pole_(of_a_function) – Martin R Jul 14 '22 at 05:57
  • @ Martin R: thank you for this link! I had started reading this link myself and got really confused about the meaning of "Holomorphic Functions". A Holomorphic Function is a complex function made of multiple variables such that the function is "complex differentiable". I am assuming that this is equivalent to a function being "differentiable" in the standard setting? thank you so much! – stats_noob Jul 14 '22 at 06:01
  • 6
    Antonoyaro, I suggest you do some more thorough research - chase every relevant Wikipedia link that is shown on every relevant page. Complex differentiability is the same idea as real differentiability, but the conditions for it to hold are much stricter, and the consequences of being holomorphic/analytic/complex differentiable are much stronger. For example, holomorphic functions are automatically infinitely differentiable. The Wikipedia article explains the definition of a pole in good detail, but it isn’t as simple a definition as “dividing by zero” – FShrike Jul 14 '22 at 06:27
  • Please check my edit - your original formatting was wrong, I’ve corrected it to what I think you meant – FShrike Jul 14 '22 at 06:29
  • 3
    I strongly recommend you open a complex analysis book— there are several that approach the subject from an elementary position. The reason why I recommend this is because a solid grasp of a classification of singularities (e.g., a pole) requires a mastery of the fundamentals of holomorphicity/analycity, which is much more subtle than real differentiability in several ways. –  Jul 14 '22 at 06:37
  • 1
    I agree with @William ... Talking about formulas with things like $\int ^{i\infty}_{-i\infty}$ presupposes you know about complex analysis. There are undergraduate-level complex analysis texts. – GEdgar Jul 14 '22 at 10:44

2 Answers2

2

What exactly is a "pole" of a function?

The point $z_{0}$ is an isolated singularity of $f(z):\mathbb{C}\mapsto\mathbb{C}$ if $f(z)$ is analytic in $0 < |z-z_{0}| < r$, which is a punctured disk of radius $r$ centered at $z_{0}$ but not analytic at $z_0$. A pole is a type of isolated singularity.

A complex function $f(z)$ has a pole of order $m$ at a point $z_{0}$ if $m$ is the largest positive integer such that $a_{-m} \ne 0$ where $a_n$ is the coefficient in front of the term with power $n$ in $f(z)$’s Laurent series. A pole of order one is a simple pole. A pole of order two is a double pole, etc. The limit to a pole “exists” and is infinite.

Intuitively, you can think of a pole as a vertical asymptote in the complex plane. It turns out that when you integrate along a closed contour in the complex plane, the path you travel is only dependent on the residues of the poles inside the contour. This is known as the residue theorem.

We calculate the residue of a function at a pole through either the limit formula or, if one expands a function $f(z)$ in a Laurent series about the point $z_{0}$, we can look at the coefficient with power $-1$ to find the residue.

Example: $$f(z) = \frac{1}{(2z-5i)^{69}}$$ has a pole of order 69 at $z=\frac{5i}{2}$.

Once you have determined the "pole" of a function - how do you determine that the "pole" of the function 1/(s+1) is on the left half of the plane?

Well, for the inverse Laplace transform, we use a Bromwich contour, which is a straight line on the positive real axis and what usually is a large semicircle that connects the ends of the line. We determine how far on the positive real axis we need to set the straight line based on the poles of $f(z)$, such that when we draw the contour it encompasses every single pole.

enter image description here

Sometimes you might encounter a branch cut so you deform your path around it like this

enter image description here

Hopefully this helped. I recommend watching YouTube videos or reading Wikipedia/textbooks on complex analysis though before you try anything further.

Captain Chicky
  • 1,440
  • 4
  • 15
  • According to my understanding, your definition of a singularity (in the first paragraph) is missing some important details. – Andreas Lenz Sep 19 '22 at 06:11
  • @AndreasLenz I’ve tried my best to think on the top of my head how to define it to someone who doesn’t know what it is, so I guess it’s likely that I would miss some details. You’re welcome to edit my answer though if you can get a better explanation though! (Or something else I’m still not too sure how everything works around here idk) – Captain Chicky Sep 19 '22 at 06:13
  • 1
    Thanks for your answer :) I actually only referred to the first paragraph of your answer. I suppose you meant to also mention that $f$ has to be not analytic at $z_0$ or some kind of unboundedness. In your current answer you only mention that $f$ needs to be analytic in the open disc. – Andreas Lenz Sep 19 '22 at 09:45
0

To make it simple, a pole of a function, is simply the generalisation of a vertical asymptote when the definition domain is the complex numbers instead of real numbers. typically the $f(z) = \frac{1}{(z-z_0)...(z-z_i)}$ has poles in $z_0, ..., z_i$.

The difference is globally that if a vertical asymptote makes a wall you cannot cross with a continuous function, you can walk around a pole.

Camion
  • 289