Where I am confusing about the concept of 'weightage' and 'Balance Point'?

Question

By Balance point I understand equal weight on both sides of a lever.

Various sources, including stackexchange threads use to treat 'mean' as 'balancing point'.

We want to place a fulcrum on the line so that the line doesn't tip due to the weights.

I took a simple data set to test this.

$1, 2, 3, 4, 5$

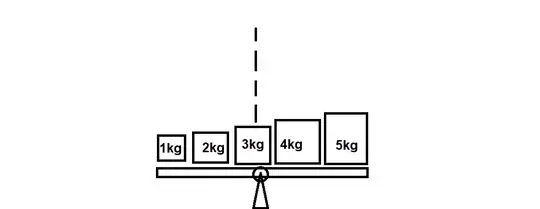My data set without any kind of break down.

1 has less weight, 2 has more weight ...

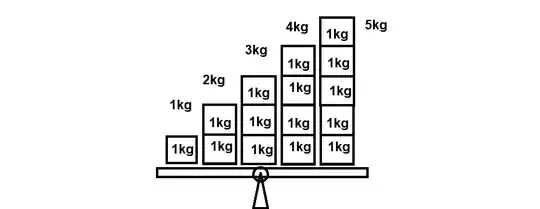
I broken down the weights or values of each data into bar chart, like 1=1 weight 2=two 1 weights stacked on each other, so on.

Here first column = total weight 1
Second column = 1+1= total weight 2
and so on.

But it strikes shockingly, as the mean or average
$(1+2+3+4+5)/5 = 15/5 =3$ looks too off to be on the balance point.

Quite visibly, there are less blocks on the left side and more blocks on the right side. To 'balance' it, I have to choose a position that divides the blocks equally.

I have made an attempt to find the balance point, just like arranging Lego blocks.

So my questions are:

a: What I am missing here? why I am failing to process 3 (mean) as the balance point?

b: in case the balance point is really different concept from mean, then is there really a name and an application of it? Is it an existing measurement of central tendency?

Answer 1

You have not understood the idea of balance because you don't understand the idea of weighting.

Your calculation has one point at 1, two data at 2, and so on to five points at 5. The mean of this is $$\frac{1+2+2+3+3+3+4+4+4+4+5+5+5+5+5}{1+2+3+4+5}=\frac{55}{15}=\frac{11}{3}$$

You should have $\frac{15}{5}=3$ instead.

Don't confuse the size of the measurement with the number of measurements of that size.

You do not have a dataset of $1, 1, 1, \dots 1$. You do not have a dataset of $1, 2, 2, \dots 5, 5, 5, 5, 5$. Both your drawings are calculating the mean of these other datasets, so of course they are getting the wrong result for the dataset $1, 2, 3, 4, 5$.

Answer 2

As mentioned in the comments, your first image shows the mean of the dataset $\{1,2,2,3,3,3,4,4,4,4,5,5,5,5,5\}$. This mean is greater than $3$, consistent with the "balancing point".

To find the mean of $\{1,2,3,4,5\}$, physically this is the same as having one piece of weight at each position $x=1,2,3,4,5$ only.

Physically the data $x$ are represented by torques applied at different $x$ positions, not of different weight/force. The frequencies of data, or the "weights" as in "weighted mean", are represented by different weight/force. The main mistake in your question is that you represent the data $x$ by both position and weight, and you scaled up the weight at each position incorrectly.

Let $\mu$ be where the weight balances, the position of the "balancing point". Consider the torque of the weights on each side, if the weight of each weight is $W$,

$$\begin{align*} (1-\mu)W+(2-\mu)W+(3-\mu)W+(4-\mu)W+(5-\mu)W &= 0\\ 1+2+3+4+5 &= 5\mu\\ \mu &= 3 \end{align*}$$

This $\mu$ is consistent with the actual mean, in this example $\mu = \dfrac{1+2+3+4+5}{5} = 3$.

Answer 3

Not a separate answer but just a visual representation of user @Peterwhy 's answer

This would be the correct arrangement that satisfy

$$\begin{align*} (1-\mu)W+(2-\mu)W+(3-\mu)W+(4-\mu)W+(5-\mu)W &= 0\\ 1+2+3+4+5 &= 5\mu\\ \mu &= 3 \end{align*}$$