What are the most efficient ways to calculate the sum of positive divisors function, σ, and aliquot sum, s?

Question

---

Given a positive integer $n$, what are the most efficient algorithms for calculating the sum of positive divisors function $\sigma_{1}(n)$ and the aliquot sum $s(n)$ ?

---

Answer 1

---

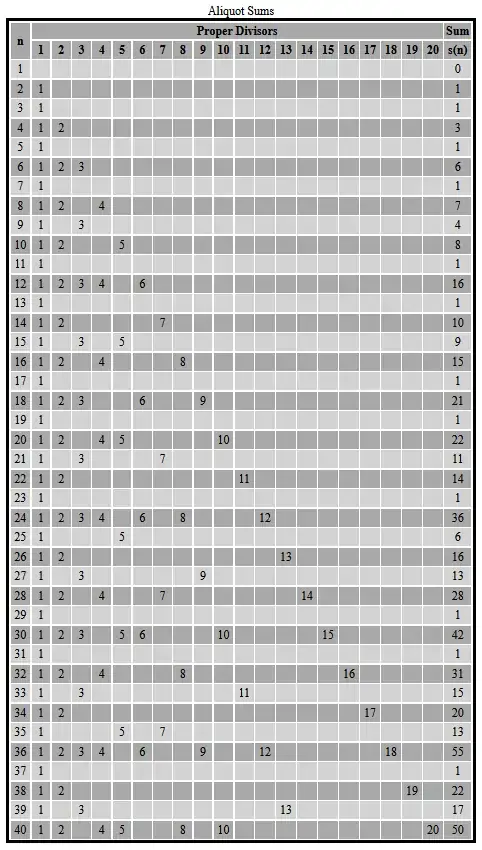
An approach similar to Eratosthenes' Sieve seems efficient, and is based upon the following table …

---

The following Java program — which is based upon the idea encapsulated in the above table — calculates the aliquot sums $s(1)$ — $s(40)$ …

public class GenerateAliquotSums
  {
  public static void main ( String [] args )
    {
    final int MAX_N = 40 ;
    final int NUM_ROWS = MAX_N + 1 ;
    final int NUM_COLS = NUM_ROWS / 2 + 1 ;
    int [] [] divisorTable = new int [NUM_ROWS] [NUM_COLS] ;
    for ( int col = 1 ; col < NUM_COLS ; col ++ )
      for ( int row = (2 * col) ; row < NUM_ROWS ; row += col )
        divisorTable [row] [col] = col ;
    for ( int row = 1 ; row < NUM_ROWS ; row ++ )
      {
      int rowSum = 0 ;
      for ( int col = 1 ; col < NUM_COLS ; col ++ )
        rowSum += divisorTable [row] [col] ;
      System.out.println ( "s(" + row + ") = " + rowSum ) ;
      } // end for
    } // end main method
  } // end GenerateAliquotSums class

---

Also follows a similar C++ program calculating aliquot sums $s(1)$ — $s(1000000)$ …

#include <iostream>
#include <vector>
using namespace std ;
const int LIMIT = 1000000 ;
int main ( void )
  {
  vector<int> s ( (LIMIT + 1), 1 ) ;
  s[0] = 0 ;
  for ( int col = 2 ; col <= (LIMIT + 1) / 2 ; col++ )
    for ( int row = (2 * col) ; row <= LIMIT ; row += col )
      s[row] += col ;
  cout << "s(" << (s.size() - 1) << ") = " << s[s.size() - 1] << endl ;
  return 0 ;
  } // end function main

---