6

Problem:
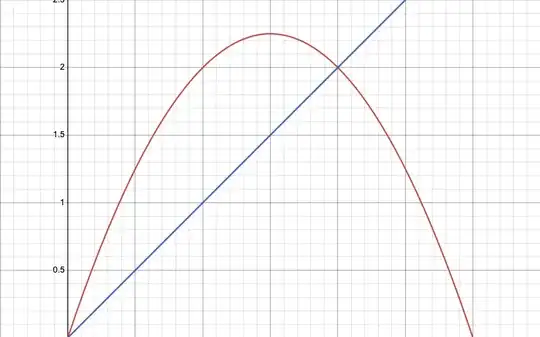
Find the volume generated when the region bounded by the given curves and line is revolved about the x-axis. $$ y = 3x - x^2$$ $$ y = 3x $$
Answer:
Let $V$ be the volume we are trying to find. The first step is to find the points where $3x - x^2$ and $y = 3x$ intersect. \begin{align*} 3x - x^2 &= x \\ -x^2 &= 2x \\ x = 0 &\text{ or } x = 2 \\ V &= \int_0^2 \pi \left( (3x - x^2)^2 - x^2 \right) \,\, dx \\ \dfrac{V}{\pi} &= \int_0^2 (3x - x^2)^2 \,\, dx - \int_0^2 x^2 \,\, dx \\ \end{align*} Now we have two integrals to evaluate. \begin{align*} \int_0^2 (3x - x^2)^2 \,\, dx &= \int_0^2 (x^2-3x)^2 \,\, dx \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \int_0^2 x^4 - 6x^2 + 9 \,\, dx \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{x^5}{5} - \dfrac{6x^3}{3} + 9x \Big|_0^2 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{32}{5} - \dfrac{6(8)}{3} + 18 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{32}{5} - 16 + 18 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{42}{5} \\ \end{align*} For the second integral we have: \begin{align*} \int_0^2 x^2 \,\, dx &= \dfrac{x^3}{3} \Big|_0^2 = \dfrac{8}{3} \\ \dfrac{V}{\pi} &= \dfrac{42}{5} - \dfrac{8}{3} = \dfrac{ 3(42) - 5(8)}{15} \\ \dfrac{V}{\pi} &= \dfrac{86 }{15 } \\ V &= \dfrac{86\pi}{15} \end{align*}

However, the book gets: $ \dfrac{ 56 \pi}{15} $.
Where did I go wrong?

Based upon a comment from John Douma, I realized that I copied the question incorrectly. Here is the revised question with my solution which still has the wrong answer.

Problem:
Find the volume generated when the region bounded by the given curses and line is revolved about the x-axis. $$ y = 3x - x^2 $$ $$ y = x $$
Answer:
Let $V$ be the volume we are trying to find. The first step is to find the points where $3x - x^2$ and $y = 3x$ intersect. \begin{align*} 3x - x^2 &= x \\ -x^2 &= -2x \\ x = 0 &\text{ or } x = 2 \\ V &= \int_0^2 \pi \left( (3x - x^2)^2 - x^2 \right) \,\, dx \\ \dfrac{V}{\pi} &= \int_0^2 (3x - x^2)^2 \,\, dx - \int_0^2 x^2 \,\, dx \\ \end{align*} Now we have two integrals to evaluate. \begin{align*} \int_0^2 (3x - x^2)^2 \,\, dx &= \int_0^2 (x^2-3x)^2 \,\, dx \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \int_0^2 x^4 - 6x^2 + 9 \,\, dx \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{x^5}{5} - \dfrac{6x^3}{3} + 9x \Big|_0^2 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{32}{5} - \dfrac{6(8)}{3} + 18 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{32}{5} - 16 + 18 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{42}{5} \\ \end{align*} For the second integral we have: \begin{align*} \int_0^2 x^2 \,\, dx &= \dfrac{x^3}{3} \Big|_0^2 = \dfrac{8}{3} \\ \dfrac{V}{\pi} &= \dfrac{42}{5} - \dfrac{8}{3} = \dfrac{ 3(42) - 5(8)}{15} \\ \dfrac{V}{\pi} &= \dfrac{86 }{15 } \\ V &= \dfrac{86\pi}{15} \end{align*}

However, the book gets: $ \dfrac{ 56 \pi}{15} $.
Where did I go wrong?

Here is an updated answer based upon the comments from DougM.

Answer:
Let $V$ be the volume we are trying to find. The first step is to find the points where $3x - x^2$ and $y = x$ intersect. \begin{align*} 3x - x^2 &= x \\ -x^2 &= -2x \\ x = 0 &\text{ or } x = 2 \\ V &= \int_0^2 \pi \left( (3x - x^2)^2 - x^2 \right) \,\, dx \\ \dfrac{V}{\pi} &= \int_0^2 (3x - x^2)^2 \,\, dx - \int_0^2 x^2 \,\, dx \\ \end{align*} Now we have two integrals to evaluate. \begin{align*} \int_0^2 (3x - x^2)^2 \,\, dx &= \int_0^2 (x^2-3x)^2 \,\, dx \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \int_0^2 x^4 - 6x^3 + 9 \,\, dx \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{x^5}{5} - \dfrac{6x^4}{4} + 9x \Big|_0^2 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{32}{5} - \dfrac{6(16)}{4} + 18 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{32}{5} - 24 + 18 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{2}{5} \\ \end{align*} For the second integral we have: \begin{align*} \int_0^2 x^2 \,\, dx &= \dfrac{x^3}{3} \Big|_0^2 = \dfrac{8}{3} \\ \dfrac{V}{\pi} &= \dfrac{2}{5} - \dfrac{8}{3} = \dfrac{ 6 - 24}{15} \\ \dfrac{V}{\pi} &= -\dfrac{18 }{15 } \\ V &= -\dfrac{18\pi}{15} \end{align*} This answer is obviously wrong.
The book gets: $ \dfrac{ 56 \pi}{15} $.
Where did I go wrong?

Here is an updated answer based upon the comment from N. F. Taussig. I now have a correct solution.

Answer:

Let $V$ be the volume we are trying to find. The first step is to find the points where $3x - x^2$ and $y = x$ intersect. \begin{align*} 3x - x^2 &= x \\ -x^2 &= 2x \\ x = 0 &\text{ or } x = 2 \\ V &= \int_0^2 \pi \left( (3x - x^2)^2 - x^2 \right) \,\, dx \\ \dfrac{V}{\pi} &= \int_0^2 (3x - x^2)^2 \,\, dx - \int_0^2 x^2 \,\, dx \\ \end{align*} Now we have two integrals to evaluate. \begin{align*} \int_0^2 (3x - x^2)^2 \,\, dx &= \int_0^2 (x^2-3x)^2 \,\, dx \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \int_0^2 x^4 - 6x^3 + 9x^2 \,\, dx \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{x^5}{5} - \dfrac{6x^4}{4} + \dfrac{9x^3}{3} \Big|_0^2 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{32}{5} - \dfrac{6(16)}{4} + \dfrac{9(8)}{3} \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{32}{5} - 24 + 24 \\ \int_0^2 (3x - x^2)^2 \,\, dx &= \dfrac{32}{5} \\ \end{align*} For the second integral we have: \begin{align*} \int_0^2 x^2 \,\, dx &= \dfrac{x^3}{3} \Big|_0^2 = \dfrac{8}{3} \\ \dfrac{V}{\pi} &= \dfrac{32}{5} - \dfrac{8}{3} = \dfrac{ 96 - 40}{15} \\ \dfrac{V}{\pi} &= \dfrac{56 }{15 } \\ V &= \dfrac{56\pi}{15} \end{align*} This answer matches that given in the book.

insipidintegrator
  • 6,730
Bob
  • 4,388
  • 3
  • 25
  • 57
  • 1
    Why do you have $3x-x^2=x$? Shouldn't that be $3x$? – John Douma Jun 21 '22 at 23:54
  • @JohnDouma You are right. There is a problem. I did not get the question right. I will update the post. – Bob Jun 22 '22 at 00:01
  • 1
    You are inconsistent in your curves that bound the region. You start with $y=3x$, but for most of the work, it looks like you have used $y=x.$ Anyway, $(3x-x^2)^2 = x^4 - 6x^3 + 9x^2$ and I think that is your problem. – user317176 Jun 22 '22 at 00:13
  • @DougM I believe I am now consistent with $y = x$. I will look at how I evaluate $(3x-x^2)^2$. – Bob Jun 22 '22 at 00:15
  • 1
    Note that $(3x - x^2)^2 = 9x^2 - 6x^3 + x^4$. You lost a factor of $x^2$. – N. F. Taussig Jun 22 '22 at 00:31
  • I believe my solution is now correct. If somebody could tell me that as an answer, I can accept the answer and close the question. – Bob Jun 22 '22 at 00:39
  • 1
    You forgot to change the sign of the volume in the last two terms. – N. F. Taussig Jun 22 '22 at 00:39
  • 3
    Keep in mind that you can answer your own question. You will not be able to accept your answer for $48$ hours, but the important thing is that you were able to solve the problem. – N. F. Taussig Jun 22 '22 at 00:42

1 Answers1

1

With problems like this, it is usually solved by the "Washer Method." This method deals when we have a gap about the rational axis. enter image description here

Let's have the red line be $y = 3x - x^2$ and the blue line be $y = x$. Now by looking at the graph we can see that the points of intersection are $0$ and $2$, but we can also find this by some algebra: $$\text{Let's set the two equations equal to each other: $3x-x^2 = x$} \\ x^2 = 2x \\ \text{We see $x=0$ is a solution for both sides. To find the other value, let $x\neq0$} \\ \frac{x^2}{x} = \frac{2x}{x} \\ x = 2$$ We see that are points of intersection are $0$ and $2$ by the graph and verified by algebra. Now let's look at the Washer Method. This method states: $$V = \int_a^b \pi [f(x)^2 - g(x)^2]dA$$ Let's think of $f(x)$ as the top and $g(x)$ the bottom of the area we want to calculate. $dA$ is if we are going to integrate with respect to $x$ or $y$. Since we rotation about the $x$-axis we will be integrating with respect to $x$, and the "top" will be $3x-x^2$ and the bottom will be $x$. Now we will perform the integration: $$V = \int_0^2 \pi[(3x-x^2)^2 - (x)^2]dx \\ =\pi \int_0 ^2 [(9x^2 - 6x^3 +x^4) - (x^2)]dx \\ =\pi \int_0 ^ 2 [x^4 -6x^3+8x^2]dx \\ =\pi \big[ \frac{x^5}{5} - \frac{6x^4}{4} + \frac{8x^3}{3}\big] \bigg|_0^2 \\ = \pi \big[ \frac{32}{5} - \frac{48}{2} - \frac{64}{3}\big] \\ = \boxed{\frac{56 \pi}{15}}$$

James
  • 762