Why (not how for how have been a proof) the integration of derivative of a function give us the function :| let me explain more with pictures.
like here we have the derivative of $x^2$,
but how the hell does the area of under it give us the $f(x)$
I can't understand the intuition of it or something.
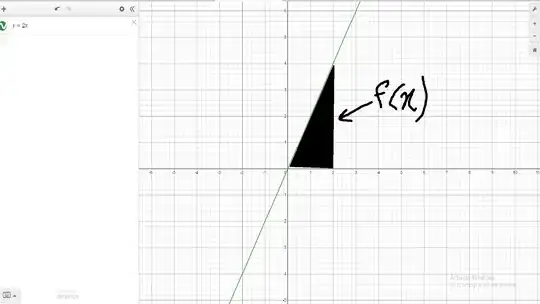
Intuitively, this is because the total is the sum of its parts.
Consider a differentiable function $f$ and let $x, y$ be such that $y=f(x)$.
The Fundamental Theorem of Calculus states that $$f(b)-f(a)=\int_{a}^{b}f'(x)dx$$ where $f'$ is the derivative of $f$.
The left hand side represents the difference between two values of $f$. The expression $f'(x)dx$ represents a small step in the $y$ direction, i.e. $dy=f'(x)dx$ and the integral sums up those small changes to get the total change.
Therefore, we can translate the above theorem to say that the total change in $f$ that occurs when $x$ goes from $a$ to $b$ can be computed by summing all of the small changes that occurred.
