Prove that $\Gamma_{abc}=\frac{1}{2}\left(\partial_bg_{ac} + \partial_cg_{ab}-\partial_ag_{bc}\right)$

Question

I am tasked with the following problem

Use the equation $$\nabla_ag_{bc}=\partial_ag_{bc}-\Gamma_{cba}-\Gamma_{bca}=0\tag{1}$$ where $$\Gamma_{abc}=g_{ad}\Gamma^d_{bc}\tag{A}$$ and the (no torsion) condition $$\Gamma_{abc}=\Gamma_{acb}\tag{i}$$ to show that $$\Gamma_{abc}=\frac{1}{2}\left(\partial_bg_{ac} + \partial_cg_{ab}-\partial_ag_{bc}\right)\tag{B}$$

To begin, I will cycle the indices in eqn. $(1)$ so that,

$$\nabla_bg _{ca}=\partial_bg_{ca}-\Gamma_{bac}-\Gamma_{cab}=0\tag{2}$$ and cycle again to obtain $$\nabla_c g_{ab}=\partial_cg_{ab}-\Gamma_{acb}-\Gamma_{abc}=0\tag{3}$$ Now, subtracting eqns. $(2)$ and $(3)$ from eqn. $(1)$ yields $$\partial_a g_{bc}-\partial_b g_{ca}-\partial_c g_{ab}-\Gamma_{cba}-\Gamma_{bca}+\Gamma_{bac}+\Gamma_{cab} + \Gamma_{acb}+\Gamma_{abc}=0$$ and rearranging gives $$\partial_a g_{bc}-\partial_b g_{ca}-\partial_c g_{ab}=\Gamma_{cba}+\Gamma_{bca}-\Gamma_{bac}-\Gamma_{cab} - \Gamma_{acb}-\Gamma_{abc}$$ Also, cycling the indices in $(\mathrm{i})$ (no torsion condition), leads to two more equations along with the original equation: $$\Gamma_{abc}=\Gamma_{acb}\tag{i}$$ $$\Gamma_{bca}=\Gamma_{cba}\tag{j}$$ $$\Gamma_{cab}=\Gamma_{bac}\tag{k}$$

Now substituting $(\mathrm{i})$, $(\mathrm{j})$ and $(\mathrm{k})$ into the expression above,

$$\partial_a g_{bc}-\partial_b g_{ca}-\partial_c g_{ab}=\Gamma_{bca}+\Gamma_{bca}-\Gamma_{cab}-\Gamma_{cab} - \Gamma_{abc}-\Gamma_{abc}$$ simplifying and rearranging gives $$\partial_a g_{bc}-\partial_b g_{ca}-\partial_c g_{ab}=2\Gamma_{bca}-2\Gamma_{cab} - 2\Gamma_{abc}$$ Rearranging, $$\Gamma_{bca} - \Gamma_{cab} - \Gamma_{abc} = \frac12 \left(\partial_c g_{ab} +\partial_b g_{ca}-\partial_a g_{bc}\right)$$

But this is not the same equation as $(\mathrm{B})$.

---

Now I will typeset the authors solution:

$$\nabla_ag_{bc}=\partial_ag_{bc}-\Gamma_{cba}-\Gamma_{bca}$$ Cycling the indices: $$\nabla_bg _{ca}=\partial_bg_{ca}-\Gamma_{\color{red}{acb}}-\Gamma_{abc}\tag{4}$$ $$\nabla_c g_{ab}=\partial_cg_{ab}-\Gamma_{\color{red}{bac}}-\Gamma_{cab}\tag{5}$$ Subtracting these two equations from the original equation gives $$\partial_a g_{bc}-\partial_b g_{ca}-\partial_c g_{ab}$$ $$=\Gamma_{cba}+\Gamma_{bca}-\Gamma_{acb}-\Gamma_{cab}-\Gamma_{bac}-\Gamma_{abc}\stackrel{\color{red}{?}}{=}-2\Gamma_{abc},$$ using the zero torsion condition. Hence the result.

1. I can't understand the author's solution for two reasons, I marked both in red in the quote above but here is why: I think the index order in eqns $(4)$ and $(5)$ are incorrect; I think the correct expressions should be $(2)$ and $(3)$.

2. Moreover, I would like to see what justifies the final equality in the author's solution quote, which can only be the case if the first four connection terms sum to zero.

---

Remark:

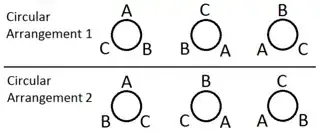
I have typed the words "cycling the indices" a lot in this question, but I didn't make it completely clear what I was doing. I am not swapping two of the three indices, instead, I am literally rotating the order of all $3$ indices. For example, if starting with say $bac$ I can obtain from it $ acb\to cba$ then one more rotation leads back to the starting point, $bac$. It is like going around a clock diagram in the counter-clockwise sense (the clockwise sense works equally well also):

Above the 'clockwise sense' is depicted by the upper version of the diagram and the 'counter-clockwise sense' is the lower part of the diagram.

---

One thing that puzzles me more than anything else is that answers and comments indicate that the solution is wrong (or has typos), so I have taken a screenshot of the author's question and solution for the sake of completeness:

Here is the question:

and here is the corresponding solution:

Answer 1

There seems to be something wrong with the cyclic renaming of indices in (2) and (3) as well as in (4) and (5). The main thing to keep in mind is that you cannot just cycle indices, but you must cyclically rename indices.

If you start with the correct equation:

$$\nabla_ag_{bc}=\partial_ag_{bc}-\Gamma_{cba}-\Gamma_{bca}$$

and you cyclically rename the indices on the lhs using $abc \to bca$ you have to do the same cyclic renaming on the rhs. You cannot just cycle indices $cba \to bac$ using the same permutation, but $cba$ becomes $acb$. So the correct expressions are:

$$ \nabla_bg_{ca}=\partial_bg_{ca}-\Gamma_{cab}-\Gamma_{acb}=0\tag{6} $$ $$ \nabla_cg_{ab}=\partial_cg_{ab}-\Gamma_{abc}-\Gamma_{bac}=0\tag{7} $$

You can also check this by keeping in mind that these are actually just dummy indices, placeholders for the multiplication with vector fields. If you check (1), you see that the index of the deriviative ($a$) always appears as the last index in the Christoffel symbols. If your derivative index is $b$ or $c$ it must also be the case that $b$ or $c$ are the last indices in the Christoffel symbols.

The same problem arises in equations (i), (j), and (k). Think about what $$\Gamma_{abc}=\Gamma_{acb}\tag{i}$$ actually means. It means that the Christoffel symbols are symmetric in the last two indices. So if you rename the indices in (i) you get $$\Gamma_{bca}=\Gamma_{bac}\tag{l}$$ $$\Gamma_{cab}=\Gamma_{cba}\tag{m}$$

If you put everything together now: $$\partial_a g_{bc}-\partial_b g_{ca}-\partial_c g_{ab}=\Gamma_{cba}+\Gamma_{bca}-\Gamma_{cab}-\Gamma_{acb} - \Gamma_{abc}-\Gamma_{bac}$$ Using (l) and (m) yields: $$\partial_a g_{bc}-\partial_b g_{ca}-\partial_c g_{ab}=-\Gamma_{acb} - \Gamma_{abc}$$ Finally, using (i): $$\partial_a g_{bc}-\partial_b g_{ca}-\partial_c g_{ab}=-2\Gamma_{abc}$$

Answer 2

You don't have to limit yourself to circular arrangement. The $a,b,c$ are just indices, they hold no significant. You can have any sort of derangement as long as you swap on both side correctly.

To understand this, suppose you actually put a value of the indices say $(a,b,c)=(1,1,1)$, then even if you had marked the indices by $(\alpha,\beta,\gamma)$ in the final evaluation you'd get the same thing. Get what I mean?

Edit: We have,

$$\nabla_ag_{bc}=\partial_ag_{bc}-\Gamma_{cba}-\Gamma_{bca}=0\tag{1}$$ and want the following: $$\nabla_bg _{ca}=\partial_bg_{ca}-\Gamma_{\color{red}{acb}}-\Gamma_{abc}\tag{4}$$

We have to replace $(a,b,c)$ with $(b,c,a)$ , so all the $a$ become $b$ , all the $b$ become $c$ and all the $c$ become a. I get by direct calculation:

$$ \nabla_{b} g_{ca} = \partial_b g_{ca}- \Gamma_{acb}-\Gamma_{cab} \tag{5}$$

Seems so there is some sort of mistake in eqtn 4.