1

You take a sphere, and inscribe it in a cylinder (so the edges are touching). You project the sphere onto the surface of the cylinder through rays emanating from the axis of the cylinder outward, orthogonally.

Now, if you 'cut open' the cylinder, for example with a vertical slice, you get a rectangular projection of the sphere with base $2 \pi r$ and height $2 r$.

That would be distorted, as moving along the axis by a distance $h$ where $-r < h < r$, the sphere's cross-section would have an arc length of $2 \pi \sqrt{r^2-h^2} $, while on the projection the same arc traced would have a length of $2\pi r$ when flat. These would only be equal at $h = 0$

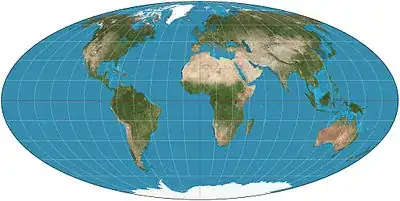
If we propose then, that we decrease the span of each one of those projections so that each arc (horizontally) has a correspondingly equal length, the output that we get is a perfect ellipse, with a ratio of $\pi$ between the major and minor axes. Is there a name for such a hypothetical projection?

I am thinking it might be the Mollweide Projection, but can't verify that.

Mollweide projection

By Strebe - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=16115320

Waleed Dahshan
  • 565

1 Answers1

1

My projection

Ok I figured out that this is not the Mollweide projection, for the reason provided by Akiva Weinberger

If we imagine that the latitude spans from $-90^\circ < \varphi < 90^\circ$ and the longitude from $ -180^\circ < \lambda < 180^\circ $, then we can map the longitude and latitude onto the $(x, y)$ plane. We let $ \lambda_0 = 0 $ signify the meridian. Therefore at a point at $(\lambda, \varphi)$ on the sphere.

$$ x = (\lambda - \lambda_0) \times r \times \cos(\varphi)$$

The last factor comes from the fact that the $ r \times \cos(\varphi) $ is the radius of the cross-section at the latitude $\varphi$. This gives us the horizontal position as function of the latitude and longitude, and in particular multiplying by the radian angle $(\lambda - \lambda_0)$ gives us the length of the arc at the height $ h $.

$$ y = r \times \sin(\varphi) $$ The height is the same as the length along the axis of the cylinder. In other words just the height $ h $

Mollweide projection

On the other hand, the equations given by the Mollweide are

$$ x = \frac{2(\lambda - \lambda_0)}{\pi} \times r \times \cos(\theta) \times \sqrt 2 $$

$$ y = r \times \sin(\theta) \times \sqrt 2$$

Differences

  1. The Mollweide projection is scaled so that the width is twice the height.
  2. In the Mollweide projection, $\theta$ is an auxiliary angle calculated by the formula: $$ 2\theta + \sin(2\theta) = \pi\sin\varphi$$

It is true, that mapping from $ (\lambda, \varphi) \to (\lambda, \theta) \to (x, y) $ is not straigh-forward. For one, $$ \alpha = f(\varphi) = \varphi + \sin(\varphi) $$ has no obvious inverse. If we let the inverse be $f^{-1}(\alpha) = \varphi$ so that $ \frac{ f^{-1}(\pi\sin\varphi) }{2} = \theta $, we have a mapping. I still lack the clarity as to what the auxiliary angle helps do.

Waleed Dahshan
  • 565