How to find $s_{xx}, s_{xy}$ from linear estimate

Question

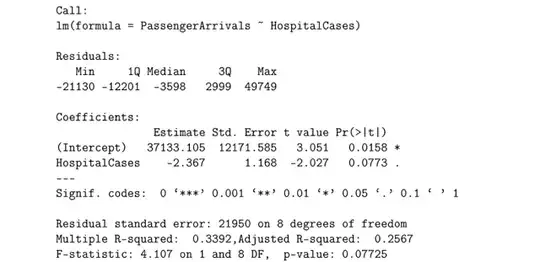
If I have the least squares estimate, can I derive either $s_{xx}$ or $s_{xy}$ from it? For example, given the following linear model:

$$-2.367=\frac{s_{xy}}{s_{xx}}$$ would give me the value for the estimate, however without either $s_{xx}$ or $s_{xy}$ known, I cannot see how I can derive this.

I am testing for the hypothesis that $$\begin{align}H_0&:\beta_1 = -4 \\ H_1&: \beta_1 \ne -4 \end{align}$$

and using the following test statitic $$T = \frac{\hat{\beta_i}-\beta_{i0}}{S\sqrt{c_{ii}}}$$

where $c_{11}= \frac{1}{s_{xx}}$, but I cannot get this from the model shown.

Additional:

$$T = \frac{\hat{\beta_i}-\beta_{i0}}{S\sqrt{c_{ii}}} = \frac{-2.367-(-4)}{1.168\sqrt{c_{11}}}$$

When not including $\sqrt{c_{11}}$ I get $t = 1.398$, with $t_{8, .025}=2.306$, there is weak evidence to reject the null hypothesis that $\beta_1 = -4$. However, I am unsure whether that I can remove $\sqrt{c_{11}}$ from the calculation.

Answer 1

Recall that if you define:

$$s_{xx} = \sum (x - \bar{x})^2 = \sum x^2 - \frac{(\sum x)^2}{n}$$ $$s_{yy} = \sum (y - \bar{x})^2 = \sum y^2 - \frac{(\sum y)^2}{n}$$ $$s_{xy} = \sum (x - \bar{x})(y - \bar{x}) = \sum xy - \frac{(\sum x)(\sum y)}{n}$$

Then the linear least-squares estimate is $y - \bar{y} = \dfrac{s_{xy}}{s_{xx}} (x - \bar{x})$ (or in slope-intercept form $y = mx + b$, then $m = \dfrac{s_{xy}}{s_{xx}}$ and $b = \bar{y} - m \bar{x}$), and Pearson's correlation coefficient is $r = \dfrac{s_{xy}}{\sqrt{s_{xx} s_{yy}}}$.

So, if you can find $s_{xx}$, you could calculate $s_{xy} = ms_{xx}$, and then $s_{yy} = \frac{m^2s_{xx}}{r^2}$. And you're given $m = -2.367$ and $r^2 = 0.3392$.

I'm having trouble figuring out a way to get $s_{xx}$, though.