Background
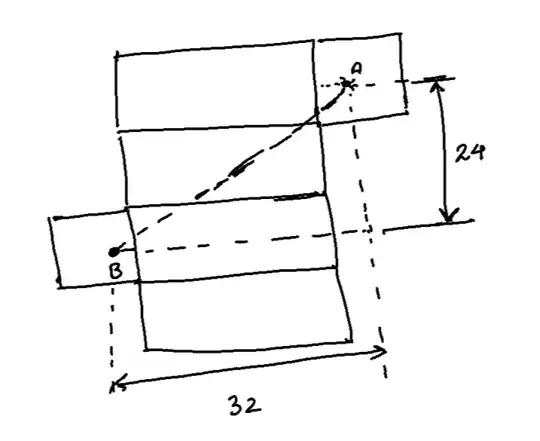
I came across this puzzle on TikTok by Henry Dudeney. There is a cuboidal room, 30 units long, 12 units wide and 12 units high. There is a spider at point A on the inside wall, 1 unit below the center of the top right edge and an insect at point B, 1 unit above the center of the bottom left edge as shown in figure 1 below. The spider can only crawl along the walls of the cube and wants to get to the fly (which doesn't move) along the shortest path.
I'll leave the answer to this puzzle and how to generalize it for any positions of the spider, fly and cuboid dimensions in an answer in case you want to think about it yourself before spoiling the puzzle.
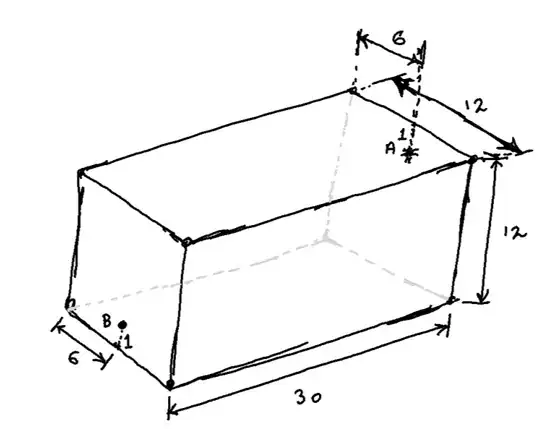 Figure-1: Original spider and insect puzzle.
Figure-1: Original spider and insect puzzle.
The question
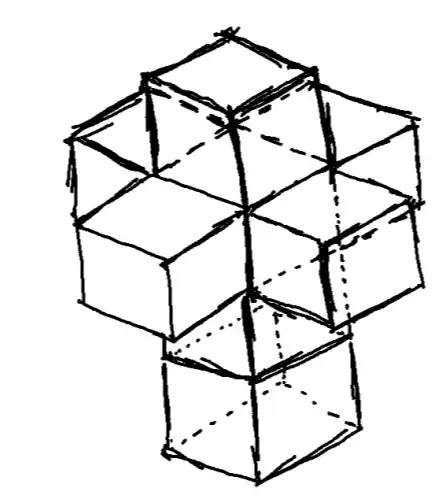
But now, what if the cuboid is replaced by a solid that is concave. For instance, the solid which is the flattened Teserract from Salvadore Dali's painting: https://en.wikipedia.org/wiki/Crucifixion_(Corpus_Hypercubus). Now imagine a spider on one of the faces of one of the cubes and the fly on another face of some other cube. Let's assume for now that the boundaries between the cubes don't exist. We now want to find a general algorithm for finding the shortest path between the spider and the fly. However, the trick we used before which involved flattening the cube doesn't apply anymore since there doesn't seem to be a way to flatten such a solid without having the faces overlap. An extension to this is to bring back the boundaries between the cubes and allow the spider to crawl on the boundaries and cross over to the cube on the other side once it reaches a common edge.