I came across a handout from a multivariable calculus class. In it, an example for the geometrical intuition underlying the Lagrange multiplier optimization method is provided. The approach is different from what I've encountered online and in the standard/textbook angle (e.g., Stewart).
My question: does this example even make sense? Allow me to elaborate.
The example is framed as follows:
The method is easier to understand if we consider the geometry behind it. We have a function f whose graph is a surface in space, and a function g that we refer to as the constraint. By this, we mean that only values on the surface of f in which we are interested are the ones that satisfy g(x,y) = k for some constant k.
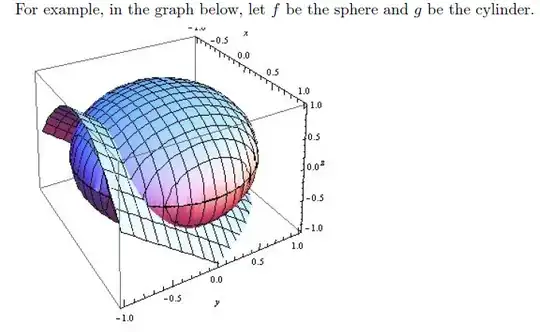
So far so good! We then get this graphic:
The author then goes on to say:
We would like to find the point (x0,y0) so that g(x0,y0) = k and f(x0,y0) yields the maximum value along all points that satisfy g(x,y) = k. Geometrically, we want to find the point (marked in black) on the intersection of the two surfaces that is at maximum height.
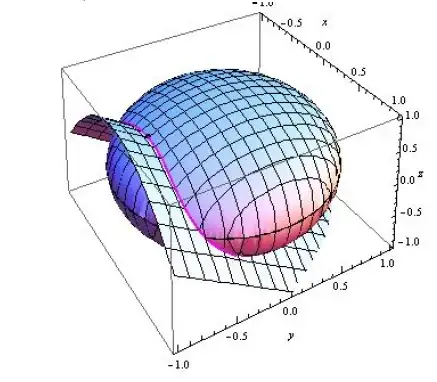
To find the coordinates of this point, let's think about the level curves on each surface. On the 3D graph, the level curves of each surface are graphed at the height of the maximum intersection:
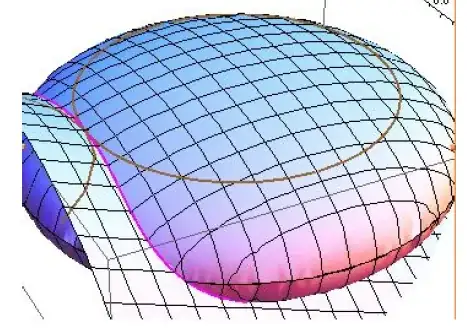
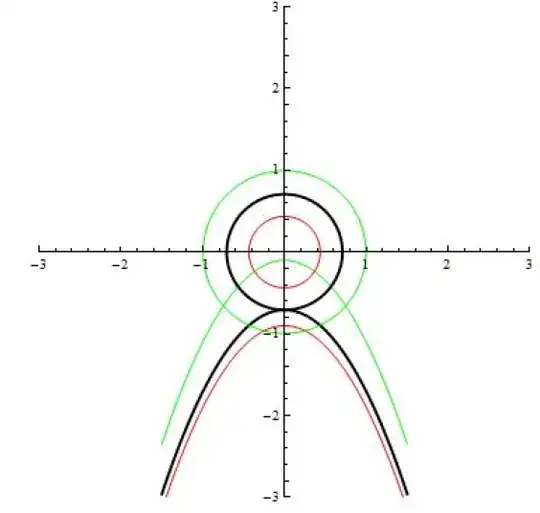
Notice that the level curves are tangent at this point; i.e. at (x0,y0,z0), the two level curves f(x,y) = z0 and g(x,y) = z0 are tangent. Let's look at the projection of some of the level curves into the xy plane.
Curves of the same color indicate level curves at the same height. Notice that the only pair of curves that are tangent are the black pair, which correspond to the two level curves graphed on the surfaces above; these curves are where the maximum occurs. This will be true in general: if f has a maximum or minimum value at (x0,y0) with respect to the constraint g(x,y) = k, then the two level curves are tangent.
Discussion
In sum, the author says that we need to find the extreme values of f subject to the constraint that g = k but she then goes on to consider the full range of g and several different level curves of g. Huh??
It seems like the approach taken here would work if we had two functions that we knew intersected, but didn't have a specific level curve constraint in mind, and wanted to maximize the value of one function provided we're on the intersection of the two. But of course there's no guarantee that two surfaces in general will intersect. For example, consider the case when g(x,y) is a sphere and f(x,y) is parabolic cone that sits directly but far above the sphere. Though the sphere and cone don't intersect, they can have a common domain, allowing one to use Lagrange's method to maximize/minimize f subject to being on a level curve of g = k. Right?
To distill this down even further: I think this is a confusing, misleading example and I'm wondering if you all agree. Thank you.