I'm reading about quantile function of a probability measure. However, I could NOT prove the property (c) $F(x) \ge t \iff x \ge F^{-1}(t)$ if $F^{-1}$ is defined with the strict inequality, i.e., \begin{align} F^{-1} (t) := &\inf \{x \in \mathbb R \mid F(x) \color{red}{>} t\} \quad (\star). \end{align}
On the other hand, everything goes well if we define \begin{align} F^{-1} (t) := &\inf \{x \in \mathbb R \mid F(x) \color{red}{\ge} t\} \quad (\star\star). \end{align}
Could you confirm if property (c) above is NOT true with defintion $(\star)$?
Let $\mu$ be a Borel probability measure on $\mathbb R$ and $F:\mathbb R \to [0, 1]$ its c.d.f. Then $F$ is non-decreasing and right-continuous. The quantile function $F^{-1}:(0, 1) \to \mathbb R$ is defined by \begin{align} F^{-1} (t) := &\inf \{x \in \mathbb R \mid F(x) \color{red}{\ge} t\}. \end{align}
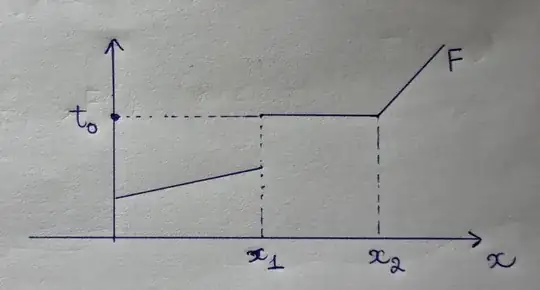
Clearly, $F^{-1}$ is non-decreasing. However, it's not necessarily true that $F^{-1}(t) = \inf \{x \in \mathbb R \mid F(x) \color{red}{>} t\}$. In below example, $F^{-1}(t_0) = x_1$ whereas $\inf \{x \in \mathbb R \mid F(x) \color{red}{>} t_0\} = x_2$.
a. $F \circ F^{-1} (t) \ge t$.
Let $(x_n)$ be a sequence in $\{x \in \mathbb R \mid F(x) \ge t\}$ such that $x_n \to (F^{-1} (t))^+$. This implies $F(x_n) \ge t$. By right-continuity of $F$, we get $F \circ F^{-1} (t) = \lim_n F(x_n) \ge t$.
b. $x \ge F^{-1} \circ F(x)$.
We have $x \in \{y\in X \mid F(y) \ge F(x)\}$, so $x\ge\inf\{y\in X \mid F(y) \ge F(x)\} =F^{-1} \circ F(x)$.
c. $F(x) \ge t \iff x \ge F^{-1}(t)$.
If $F(x) \ge t$ then $x \in A:=\{x \in \mathbb R \mid F(x) \ge t\}$. Then $x \ge \inf A = F^{-1}(t)$.
If $x \ge F^{-1} (t)$ then $F(x) \ge t$. If not, $F(x) <t$. By right-continuity of $F$, there is $y>x$ such that $F(x) < F(y)<t$. Then $y \le F^{-1} (t)$ and thus $x <y\le F^{-1} (t)$, which is a contradiction.
d. $F^{-1}$ is left-continuous.
Fix $t_0 \in (0,1)$ and let $x_0 := \sup_{t<t_0} F^{-1} (t)$. Because $F^{-1}$ is non-decreasing, $F^{-1} (t) \le F^{-1} (t_0)$ for all $t<t_0$. Hence $x_0 \le F^{-1} (t_0)$.
On the other hand, $F(x_0) \ge F \circ F^{-1} (t) \ge t$ for all $t<t_0$. Hence $F(x_0)\ge t_0$ and thus $x_0 \ge F^{-1} (t_0)$.