homotopy groups of Wu manifold

Question

I'm interested in the homotopy groups of the Wu manifold $ W=SU_3/SO_3 $. From LES homotopy we have $$ \pi_1(W)=\pi_0(SO_3)=0 $$ since $ SU_3 $ simply connected. And $$ \pi_2(W)=\pi_1(SO_3)=\mathbb{Z}_2 $$ since $ \pi_2(SU_3) $ vanishes, as it does for every lie group. Finally we have $$ \pi_3(SU_3)=\mathbb{Z} \to \pi_3(W) \to 0=\pi_2(SO_3) $$ so $ \pi_3(W) $ must be cyclic. Hopefully this question isn't to broad. I'm interested in all homotopy groups but I would especially like to know which cyclic group $ \pi_3(W) $ is. Mostly I'm just in it to learn new tricks for calculating homotopy groups of $ SU_3 $ and $ SO_3 \cong \mathbb{R}P^3 $ and seeing how these can be used to calculate homotopy groups of $ G/H $.

Answer 1

The answer is that $\newcommand{\iso}{\cong} \newcommand{\Z}{\mathbb{Z}}$ $\pi_3 W \iso \Z_4$. This is computed in Proposition 4.1 of the following paper:

Kachi, H. Homotopy groups of homogeneous space SU(n)/SO(n). J. Fac. Sci., Shinshu Univ. 13, 27-34 (1978).

Using the long exact sequence of the bundle $SU(3) \to W$, this is equivalent to showing the following:

Proposition A: the map $\pi_3 SO(3) \to \pi_3 SU(3)$ is multiplication by $\pm 4$.

From this and the fact that $\pi_4 SU(3) = 0$, we also get that $\pi_4 W = 0$.

The proof of Proposition A given in the paper of Kachi seems a bit complicated to me. Let me try to give a different (and hopefully simpler) proof. It relies on the following reformulation of Proposition A:

Proposition B: the map $H_3(SO(3); \Z) \to H_3( SU(3); \Z)$ is multiplication by $\pm 2$.

To see that Proposition A and Proposition B are equivalent, use the fact that there is a double covering $S^3 \to SO(3)$, along with the Hurewicz theorem.

Proposition B is a statement about homology, so there are many tools to approach it. I'll give one proof below, but here are some other ideas that might also work out:

• Write down a CW decomposition of $SU(3)$ that has $SO(3)$ as a subcomplex.

• Explicitely homotope the map $SO(3) \to SU(3)$ into the subspace $SU(2) \subset SU(3)$, and compute the degree of the resulting map $SO(3) \to SU(2)$.

• Use Lie-theoretic methods, such as describing the cohomology using invariant forms.

• Find an explicit submanifold of $SU(3)$ the represents the Poincaré dual to a generator of $H^3$, then compute the intersection number between $SO(3)$ and this submanifold.

These strategies all rely on some kind of geometric understanding of the manifolds in question. Since I don't have an ounce of geometric intuition in me, let me give an algebraic proof instead. The first argument that springs to my mind is to use the Serre spectral sequence of the bundle $SO(3) \to SU(3) \to W$. This requires knowing the homology of $W$, but this is fairly easy. See for example this post.

The $E^2$ page of the homological spectral sequence with $\Z$ coefficients looks like this:

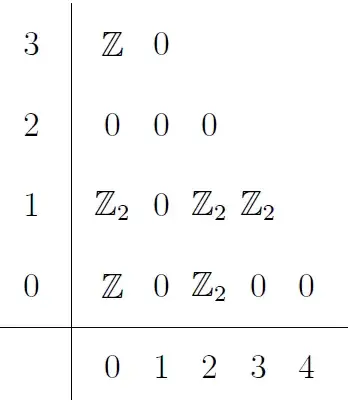
We see that there are no non-trivial differentials involving the degree $3$ diagonal. The spectral sequence machinery then gives us an exact sequence: $$ 0 \to H_3 SO(3) \to H_3 SU(3) \to \Z_2 \to 0 $$ Since $H_3 SU(3) \iso \Z$ and $H_3 SO(3) \iso \Z$, it must be that the map $H_3 SO(3) \to H_3 SU(3)$ is multiplication by $\pm 2$.