3

A body describing an ellipse of eccentricity e under the action of a force directed to focus when at the nearer apse , the centre of force is transferred to the other focus . Prove that eccentricity of the new orbit is $$\begin{align}e(\frac{3+e}{1-e})\end{align}$$ where e is eccentricity of the ellipse

My approach:-

I know that the equation of an ellipse with focus as a pole is $$\frac{l}{r}=1+e \cos{\theta}$$

And the law of force with focus as center of force is $$F=\frac{\mu}{r^2}$$

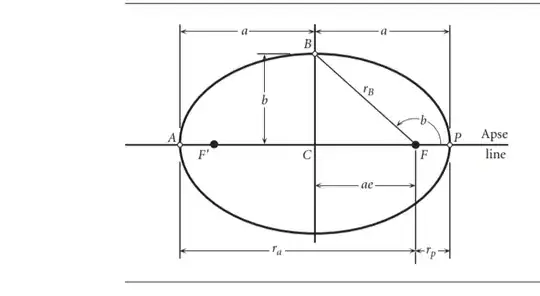Now how can I use the eccentricity of the ellipse to find the eccentricity of the newly formed path under the change of central force ? enter image description here Where $$\begin{align} r_a = \frac{r^2}{µ}\frac{1}{1-e}\end{align}$$. $$\begin{align} r_p = \frac{r^2}{µ}\frac{1}{1+e} \end{align}$$ and $$\begin{align}2a=r_a +r_p \end{align}$$ We can substitute these values back to the polar equation of ellipse to get $$\begin{align}r = a\frac{1-e^2}{1+e\cos\theta}\end{align}$$

How can we use these equations to determine the eccentricity of newly formed path after the change of focus ?

Is there any connection with newly formed path's eccentricity and the elliptical eccentricity integral ? Or can we use it as an approach ?

$$\begin{align}\int^{θ} _{0} \frac{dϑ} {(1 + e cos ϑ)^2}\end{align}$$

Bertie
  • 31

2 Answers2

4

If $a$ is the semi-major axis of the orbit and $v$ is the velocity at nearer apse, then conservation of energy and angular momentum gives: $$ av^2={\mu\over m}{1+e\over1-e}. $$ In the new orbit, velocity at nearer apse is still $v$, whereas the new semi-major axis is some $a'$, so that: $$ a'v^2={\mu\over m}{1+e'\over1-e'}. $$ where $e'$ is the new eccentricity. But $e'=c'/a'$, where $c'$ is the new focal distance, and $a'-c'=a+c$, giving: $$ a'(1-e')=a(1+e). $$ Inserting this into the previous equation gives then: $$ {\mu\over m}(1+e')=av^2(1+e)={\mu\over m}{(1+e)^2\over1-e} $$ that is: $$ 1+e'={(1+e)^2\over1-e}, $$ which is equivalent to the formula to be proved.

Intelligenti pauca
  • 55,765
2

Take into account that the ellipse changes, the angular momentum changes from $L=rv$, $v=r\dot\phi$, to $L'=r'v$ with $r=(1-e)a$ and $r'=(1+e)a$.

The solution changes from $$ \frac1r=\frac{\mu}{L^2}+c\cos(\phi-\phi_0)=\frac{1+e\cos(\phi-\phi_0)}{r^2v^2/\mu} $$ to $$ \frac1{r'}=\frac{μ}{L'^2}+c'\cos(ϕ−ϕ_0')=\frac{1+e'\cos(ϕ−ϕ_0')}{r'^2v^2/\mu}. $$ As both orbits are in periapsis at the same point, $\phi=\phi_0=\phi_0'$, this gives $$ (1-e)av^2= μ (1+e),~~~(1+e)av^2=μ(1+e') \\ \implies (1+e)^2=(1+e')(1-e) \\ 3e+e^2=e'(1-e) $$

Lutz Lehmann
  • 131,652