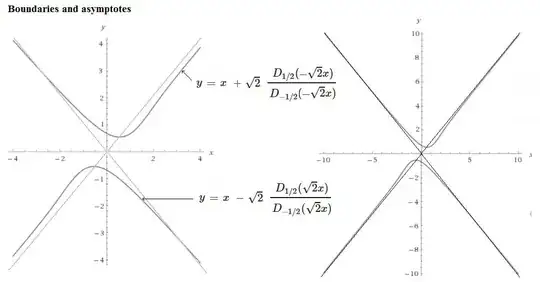
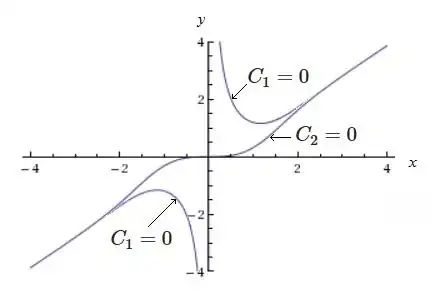
Consider the following first order ODE: $$\frac{\operatorname{d}\!y}{\operatorname{d}\!x} = x^2 - y^2$$ Despite the fact that this ODE has a very simple expression, it is not solvable in terms of elementary functions. (We need the so-called Bessel function $J_u(z)$, where $u \in \mathbb{R}$ and $z \in \mathbb{C}$.)
I've used AutoGraph to plot the direction field and to plot several integral curves.
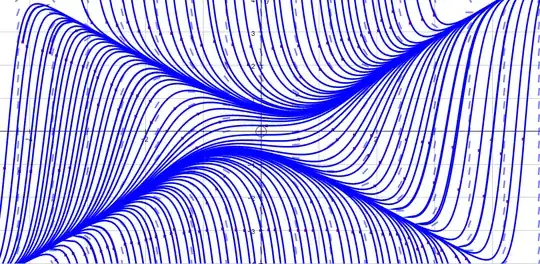
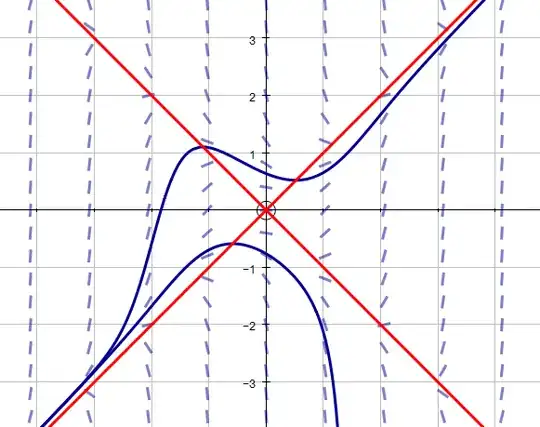
There is a clear separation of the plane. Your eye will no-doubt pick out two very heavily coloured curve-like regions. The underlying curves form a bifurcation set: choosing points on either side give qualitatively different integral curves through those points.
Is there a general way to find an equation or a parametrisation for the bifurcation set? Or do we have to be able to solve the ODE explicitly?
If it isn't possible to find the bifurcation set explicitly, then is there any way to find other information, e.g. how many regions the bifurcation set separates the plane into? (In my example, the plane is separated into three regions.)
Addendum: Here's a plot to show that the lines $y = \pm x$ ($x^2-y^2=0$) have no local significance to the integral curves. They lines $y=\pm x$ do seem to be asymptotes for some of the integral curves.