4

Diagram of the problem

Source: Tristan Needham VDG

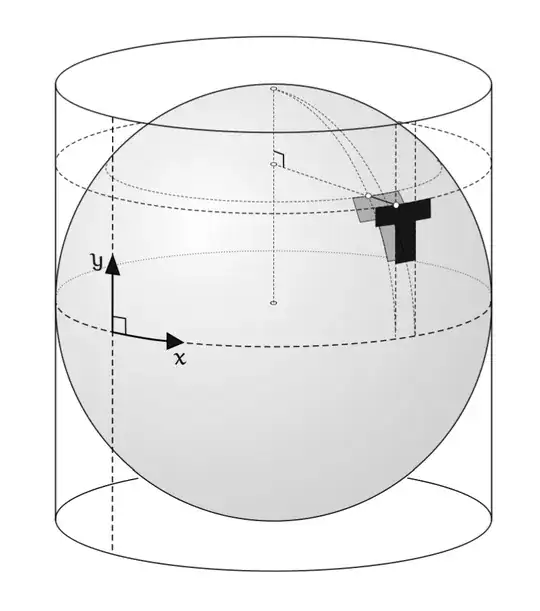
I've been trying to determine the metric for the projection of a sphere onto a cylinder, where $0 \leq x \leq 2\pi R$ and $-R \leq y \leq R$

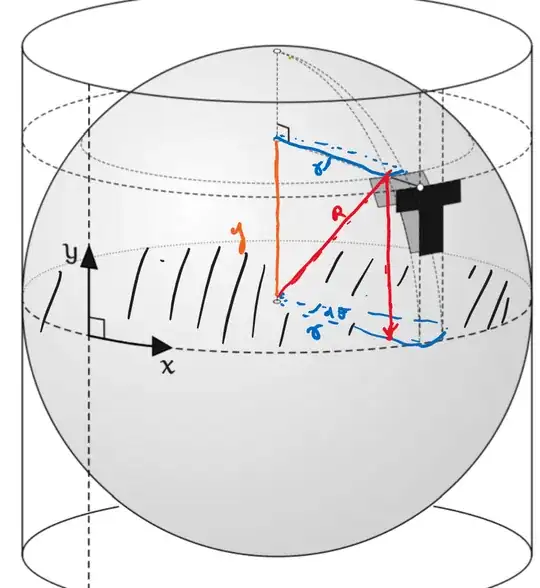
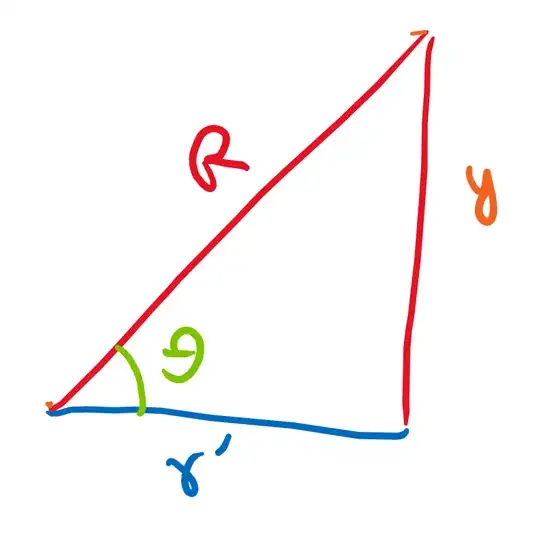
The book says to reason geometrically that $d\hat{s}^2 = \frac{\,dy^2}{R^2-y^2} + (R^2-y^2)\,dx^2$ where $d\hat{s}$ is the infinitesimal displacement on the sphere.

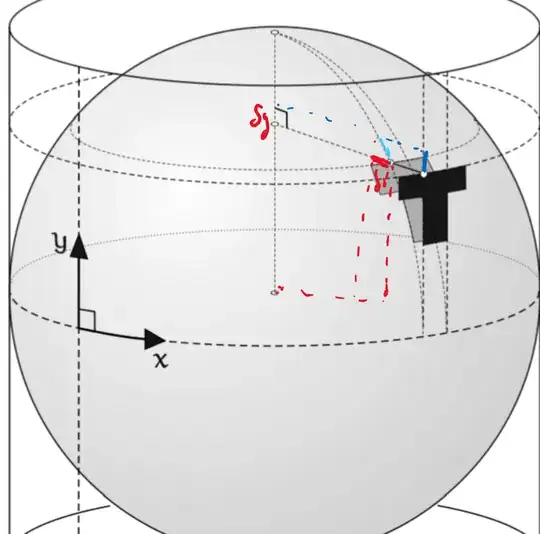
I keep getting stuck at trying to determine what the individual changes $d\hat{s_1}$ due to $dx$ and $d\hat{s_2}$ due to $dy$ are, but I keep ending up with an $R^2$ in the denominator of the $dx$ term and an $R^2$ in the numerator of the $dy$ term.

Any help would be greatly appreciated, I've beens staring at this one for quite a while!

EDIT: I have discovered in the Errata for the book that my original solution was actually correct. Thank you everyone for taking the time to address my question!

Clemens Bartholdy
  • 14,222
Ali Shakir
  • 43
  • If $x$ is the angle, it should go from $0$ to $2\pi$? – Ted Shifrin Apr 11 '22 at 23:25
  • 2
    If $x$ and $y$ are distance measurements then you need those extra factors of $R^2.$ The formula you wrote is clearly wrong at the equator, where $y=0$, because the given formula then says $d\hat{s} = \frac1{R^2}(dy)^2 + R^2(dx)^2,$ whereas the correct equation (at the equator) is $(d\hat{s})^2 = (dy)^2 + (dx)^2.$ Also, $-2\pi R \leq x \leq 2\pi R$ is a total distance $4\pi R,$ which would wrap around the cylinder twice. – David K Apr 12 '22 at 00:55
  • @DavidK, now that I think about it, you are right, in the limiting case near the equator that extra factor has to be there. I suppose there's a typo in the book? Thanks for the response, really appreciate it. And yes, the bounds on $x$ were a typo on my part. It should in fact range from $0$ to $2\pi R$ only – Ali Shakir Apr 12 '22 at 04:00
  • @TedShifrin Thanks for the correction, have edited it to be consistent. That was a typo on my part! – Ali Shakir Apr 12 '22 at 04:01
  • This still makes no sense to me. Is $x$ a coordinate on the $x$-axis or is it really $\theta$? What book is this? – Ted Shifrin Apr 12 '22 at 04:03
  • @TedShifrin this is Tristan Needham's "Visual Differential Geometry and Forms". $x$ is actually the distance traveled along a latitude of the cylinder, so in terms of $\theta$ it would be $R \theta$ – Ali Shakir Apr 12 '22 at 04:10
  • 2
    You’re also missing the square in $d\hat s^2$. I think cylindricsl coordinates are less confusing. I actually don’t understand what “metric for the projection” is supposed to mean. Is the goal to see that the projection is area-preserving? – Ted Shifrin Apr 12 '22 at 04:15
  • The final goal is to demonstrate that the projection is area-preserving and also show the area of a polar cap geometrically. By metric, in terms of $dx$ and $dy$ as defined on the cylinder, the question asks for $d\hat{s}$, the displacement on the sphere – Ali Shakir Apr 12 '22 at 04:20
  • I love this book! – Clemens Bartholdy Apr 12 '22 at 04:28
  • @Buraian it's such a wonderful book that I hesitate to consider that this question has a typo! Although the book is quite new relatively speaking. – Ali Shakir Apr 12 '22 at 04:33
  • Your formula is the metric tensor, not $ds$. – Ted Shifrin Apr 12 '22 at 04:49
  • Send me a message in this room if you want to discuss the book. I too am going through it. – Clemens Bartholdy Apr 12 '22 at 04:52

2 Answers2

3

enter image description here

In the above picture, suppose I fix $y$ and rotate $r$ by $d \theta$, what is the length gained?

$ \delta s= r' \delta \theta$

For that, we go back to highschool trignometry and draw a diagram:

enter image description here We can write:

$$ r' = \sqrt{R^2 - y^2} \tag{1}$$

Putting that back in the distance equation:

$$ \delta s = \sqrt{R^2 - y^2} \delta \theta$$

Or,

$$ \frac{ \delta s}{\delta \theta} = \sqrt{R^2-y^2} \tag{2}$$

Next we need to check how much distance is gained when $y$ is increased, in (1), we can take the differential: $$ \delta r'= \frac{-2y \delta y}{\sqrt{R^2 -y^2}} \tag{3}$$

What does $\delta r'$ represent? The shrinking of the radius of circle as we increase $y$:

enter image description here

The arclength (light blue) should be:

$$\delta s = \sqrt{\delta y^2-\delta r^2} \tag{4}$$

Using (3) in (4) , we have:

$$ \delta s = \frac{ R^2\delta y}{\sqrt{R^2-y^2}}$$

Or,

$$ \frac{\delta s}{\delta y} = \frac{R^2}{\sqrt{R^2 -y^2}}$$

Since geometrically we can see that the metric is orthogonal (page-37), we can write:

$$ ds^2 = \frac{R^2dy^2}{R^2-y^2} + (R^2-y^2)d \theta^2$$

Clemens Bartholdy
  • 14,222
2

Vectorially,

$ \vec{r_C }= ( R \cos(x), R \sin(x) , y ) $

Its projection on the sphere is

$ \vec{r_S} = ( \sqrt{R^2 - y^2} \cos(x), \sqrt{R^2 - y^2} \sin(x) , y ) $

Then, taking the differentials,

$ d \vec{r_S} = \left( \dfrac{d \vec{r_S}}{dx} \right) dx + \left( \dfrac{d \vec{r_S}}{dy} \right) dy $

and this evaluates to

$ d \vec{r_S} = \left( \sqrt{R^2 - y^2} (-sin(x) ), \sqrt{R^2 - y^2} \cos(x), 0 \right) dx + \left( -\dfrac{y\cos(x)}{\sqrt{R^2 - y^2}} , - \dfrac{y\sin(x)}{\sqrt{R^2 - y^2}} , 1 \right) dy $

Since the vector multiplying $dx$ is orthogonal to the vector multiplying $dy$ , then

$ \|d \vec{r_S} \|^2 = (dx)^2 (R^2 - y^2) + (dy)^2 ( \dfrac{y^2}{R^2 - y^2} + 1 ) $

And this simplifies to

$ \| d \vec{r_S} \|^2 = (dx)^2 (R^2 - y^2) + (dy)^2 \dfrac{R^2}{R^2 - y^2} $