Real part of roots of monic polynomial with coefficients in [0,1] is less than golden ratio

Question

I am trying to solve the following problem: Consider $n\geq 2$ and the polynomial $$P(x)=x^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\ldots+a_1x+a_0$$ with $a_{n-1}, a_{n-2},\ldots,a_1, a_0\in[0,1]$. Prove that if $P(z)=0$, then $\Re(z)<\dfrac{1+\sqrt{5}}{2}$. ($\Re(z)$ denotes the real part of the complex number $z$).

I can't seem to find a meaningful way to use the condition $a_i\in[0,1]$. I managed to prove that if $P(z)=0$, then $|z|<2$: $$|z|^n=|a_{n-1}z^{n-1}+a_{n-2}z^{n-2}+\ldots+a_1z+a_0|\leq\sum_{k=1}^{n-1}|z|^k$$ hence, if $|z|>1$, $$|z|^n\leq\frac{|z|^n-1}{|z|-1}\Rightarrow |z|^{n+1}\leq 2|z|^n-1\Rightarrow |z|<2-\frac{1}{|z|^n}$$ and so, $|z|<2$.

Also, we see here another bound for $|z|$ in terms of the positive coefficients, but, nonetheless, I couldn't find anything about $\Re(z)$.

Answer 1

Let $g=\frac{1+\sqrt 5}{2}$ be the golden ratio. Note that for $n \ge 2$ one has $g^n (g-1)=g^{n-1}>g^{n-1}-1$ so $g^n >1+g+\ldots +g^{n-2}$

But now assume by contradiction that the equation above has a root $\Re z \ge g$; dividing by $z^{n-1}$ one has:

$$ |z+a_{n-1}|=|-a_{n-2}/z-\ldots-a_0/z^{n-1}| \le 1/|z|+\ldots +1/|z^{n-1}|$$

But now $\Re(z+a_{n-1}) \ge \Re z >0$ and the imaginary parts are same so $|z| \le |z+a_{n-1}|$ so by substituting and simplifying we get

$$|z|^n \le 1+|z|+\ldots+|z|^{n-2}$$

But now the equation $x^n=1+\ldots+x^{n-2}$ has only one positive root $r_n$ (division by $x^n$ shows that clearly as rhs decreases then strictly), and from the left one has $0<x<r_n$ implies $x^n <1+x+\ldots +x^{n-2}$ (while from the right we have the opposite inequality). So, $r_n <g \le |z|$ on one hand by the first paragraph, and $|z| \le r_n$ by the inequality above which is a contradiction, and we are done!

Answer 2

This is inspired by the inequality $g^n > g^{n-2} + \cdots + 1$ in Conrad's excellent answer.

Let $g = \frac{1+\sqrt{5}}{2}$ as in his answer. Consider the polynomial

$$Q(x) = (x-a_{n-1})P(x) = x^{n+1} + \sum_{k=0}^{n-1} b_k x^k $$ where $b_k = \begin{cases} a_{k-1} - a_{n-1} a_k & k > 0\\-a_{n-1}a_0, &k = 0\end{cases}$.

Since all $a_k \in [0,1]$, all $|b_k| \le 1$. For $z \in \mathbb{C}$ with $|z| = g$, we have

$$\left|\sum_{k=0}^{n-1} b_k z^k \right| \le \sum_{k=0}^{n-1} g^k = \frac{g^n - 1}{g-1} < \frac{g^n}{g-1} = g^{n+1} = |z^{n+1}|$$

By Rouché's theorem, all roots of $Q(z)$ and hence all roots of $P(z)$ belongs to the open disc $|z| < g$. As a result, all roots of $P(z)$ have $\Re z < g$.

Update - an improved upper bound $\Re(z) \le u_* \sim 1.214497857615758$.

Let $z$ be any root of $P(x)$ outside unit disc (ie. $|z| > 1$). Let $$c_k = \begin{cases}a_{n-k}, & 1 \le k \le n\\ 0, & k > n\end{cases} \quad\text{ and }\quad \epsilon = 2c_k - 1\quad\text{ for all } k $$ Since all $c_k \in [0,1]$, all $|\epsilon_k| \le 1$. Using the fact $P(z)= 0$, we have

$$0 = \frac{2}{z^n}P(z) = 2 + \sum_{k=1}^\infty \frac{2c_k}{z^k} = 2 + \sum_{k=1}^\infty \frac{1+\epsilon_k}{z^k} = \frac{2z - 1}{z-1} + \sum_{k=1}^\infty \frac{\epsilon_k}{z^k} $$ This leads to $$\left|\frac{2z-1}{z-1} \right| = \left|\sum_{k=1}^\infty \frac{\epsilon_k}{z^k} \right| \le \sum_{k=1}^\infty \frac{1}{|z|^k} = \frac{1}{|z|-1} $$ This implies all roots of $P(x)$ lies inside a region "bounded" by the curve $$|z| = 1 + \left|\frac{z-1}{2z-1}\right|$$

Expand $z$ as $u + iv$ and using a CAS, we find this curve is part of an octic curve (the outer portion of the red curve in the illustration below): $$4v^8+16u^2v^6-8uv^6-8v^6+24u^4v^4-24u^3v^4-20u^2v^4+20uv^4-4v^4+16u^6v^2-24u^5v^2-16u^4v^2+40u^3v^2-20u^2v^2+4uv^2-v^2+4u^8-8u^7- 4u^6+20u^5-16u^4+4u^3 = 0$$

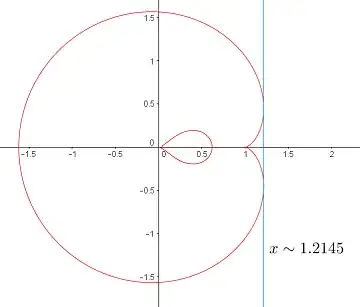
As one can see, the $u$ in this curve doesn't reach $g$. Instead, it lies inside a half-plane $\Re z \le u_*$ for some $u_* \sim 1.2$. With help of a CAS again, we find $u_*$ is a root of the heptic polynomial $$2048u^7-19456u^6+52608u^5-62848u^4+36752u^3-10288u^2+1392u-171 = 0$$ with a more accurate estimate $u_* \sim 1.214497857615758$.