1

I have the following question on the convergence of numerical optimization algorithms. When it comes to convex functions, it can be shown that algorithms like gradient descent converge after an infinite number of iterations:

enter image description here

Furthermore, the above equation suggests that after a large number of iterations, the optimal solution will be found, seeing as the difference between the solution returned at the $k$-th iteration (where $k$ is large) and the true optimal solution (i.e., "global minimum") of the function will be $0$.

Unfortunately, such convergence results are said to be generally non-existent for non-convex functions. When optimizing non-convex Functions, we usually consider ourselves lucky if the optimization algorithm even converges to a "local minimum" — if at all.

This leads to my question regarding the convergence of optimization algorithms on non-convex functions:

  • In a very general sense, are Optimization Algorithms (e.g. gradient descent, stochastic gradient descent, evolutionary algorithms, etc.) said to always (theoretically) converge to some value (e.g. even a saddle point) after an infinite number of iterations - regardless of the function being optimized? Or is it possible for an optimization algorithm to "bounce around" forever, and not display any type of convergence (even to a sub-optimal solution) even after an infinite number of iterations?

From a more layman's perspective — if I had a very powerful computer, regardless of the function I wanted to optimize, if I left the computer running for a very long amount of time: would the difference in successive iterations eventually become 0 (i.e. reach some stationary point)?

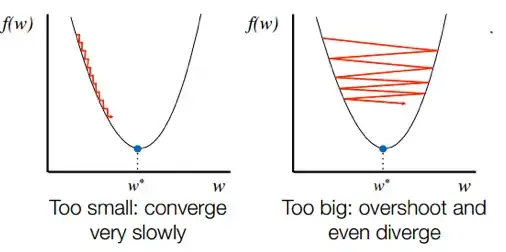
Note 1: Illustration of "Bouncing Around" - Is there any guarantee that an Optimization Algorithm WILL NOT "Bounce Around" forever, regardless of the function being optimized?

enter image description here

Note 2: In this video by Julius Pfrommer, at 5:37, the author suggests that even for convex functions - gradient descent is not guaranteed to converge (i.e., it might never converge), and that an additional line search might be required for convergence (to any point). This makes me think that perhaps some functions exist in which optimization algorithms might truly "bounce around" forever?

Note 3: I still find it hard to believe that even after an infinite number of iterations, it is possible for an optimization algorithm to have still not have found some stationary point. I wonder if there is a mathematical proof that demonstrates that an optimization algorithm will always find some stationary point (e.g. saddle point, local minimum, global minimum) after an infinite number of iterations?

Rodrigo de Azevedo
  • 23,223
stats_noob
  • 4,107

1 Answers1

4

There are certainly algorithms (natural ones, even!) that do not converge no matter how long you run them.

The classic example is when you have a measure $f(x)$ describing the error to your target, so that you want to minimize $|f(x)|$. If $f(x)$ has a root, then that root is a minimum, so the question reduces to finding roots of arbitrary functions. One common function for this is Newton's method, which approximates $f(x)$ as $f(x_n)+f'(x_n)(x-x_n)$, solves for $x$, and then repeats. But a common example that appears in many calculus textbooks is that, for a poorly chosen starting point and $f(x)$ a cubic, Newton's method will just alternate between two values, rather than converge to a root.

Jacob Manaker
  • 10,173