I am new on this forum and I hope that I will provide useful answer to mathematics problems that people might have to face in the future. Also, I do want to meet mathematicians from all over the world aha
I am currently discovering Matlab Simulink to simulate a system of non-linear differential equations. I succeeded in building a block-structure system. However, there is no one in my close circle that can provide me constructive feedback on it because they do not have, unfortunately, the skills to do so.
The system that I am trying to simulate came from :
Portaluri, Alessandro & Paparella, Francesco & Alma, Alberto & Lessio, Federico. (2020). A mathematical model for Flavescence dorée epidemiology.
There is also a more complete version in :
Lessio, Federico & Portaluri, Alessandro & Paparella, Francesco & Alma, Alberto. (2014). A Mathematical Model of Flavescence Dorée Epidemiology. Ecological Modelling. 312. 10.1016/j.ecolmodel.2015.05.014.
Here is the system :
With, $$ \begin{aligned} S_0 &= 5800 \\ I_0 &= 200 \\ G_0 &= 0 \end{aligned}\quad \begin{aligned} D &= 6000 \\ k_i,~~\epsilon,~~q &= \text{ constants} \\ \tau &= 1 \end{aligned} $$ So, \begin{align} S' &= -qS(pI+\epsilon)^2+k_1I+k_4G \\ I' &= ~~qG(pI+\epsilon)^2-k_1I-k_3I \\ G' &= -qG(pI+\epsilon)^2-k_4G+\tau^{-1}(D-S-I-G) \end{align}
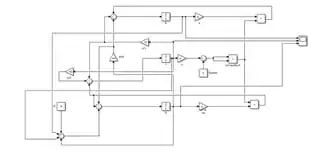
Here is the Simulink block model that I built.
Please feel free to give me some feedback and criticism, so I can know if I produced bad work or not.
Thanks you all,
Hugo