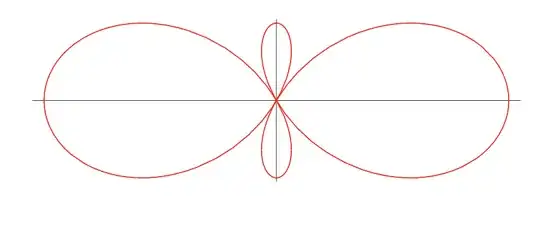
Ceva Cycloid polar coordinates form is: $$ r = 1 + 2\cos(2\phi) $$
I found that the relation between polar and Cartesian coordinates can be expressed:
$$ x = r\cos\phi, y = r\sin\phi $$
I need to express Ceva Curve as a parametric equation of the form: $$ a(t) = (f(t), g(t)) $$
The purpose is that I can draw Ceva Curve as a raster image, programmatically. $a(t)$ could be treated as function of time.
I'd be very grateful for instructions.
Cycloid of Ceva: