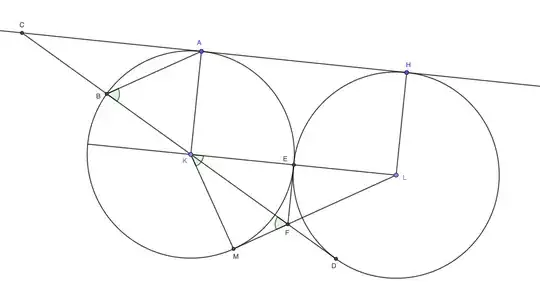
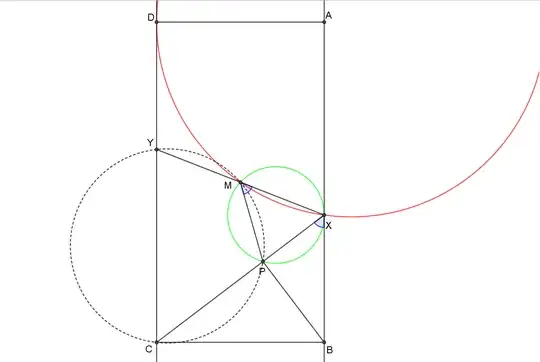
Given two circles with centers $K$, $L$, externally tangent at $E$, with common tangent $AH$ and tangent $LM$, join $MA$, make chord $MB=MA$, and draw $BD$ tangent to the other circle.
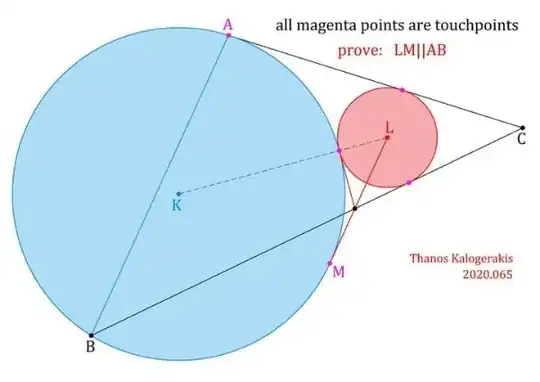
Since triangle $ABM$ is isosceles, then $\angle BAM=\angle MBA$. And since $\angle LMA$ between chord and tangent is equal to $\angle MBA$ in the alternate segment, then$$\angle LMA=\angle BAM$$Therefore$$LM\parallel AB$$
Note: On this interpretation of the question and its conditions, tangents $AH$ and $BD$ are extraneous. But even if the tangents are included, and $A$ is therefore not random, $B$ cannot be supposed random, but must be chosen such that triangle $ABM$ is isosceles. In other words, $M$ is the midpoint of arc $AMB$. Otherwise $LM$, which is given in position for the given circles, will not be parallel to $AB$. A fuller statement of the conditions in this question would be helpful.
Addendum:
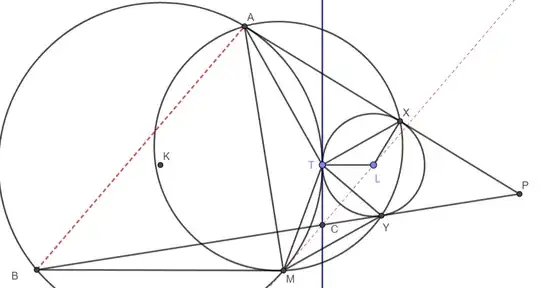
In light of the clarifying comments, that the above solution misinterprets the question, let me offer at least a proof for the special case of equal circles.
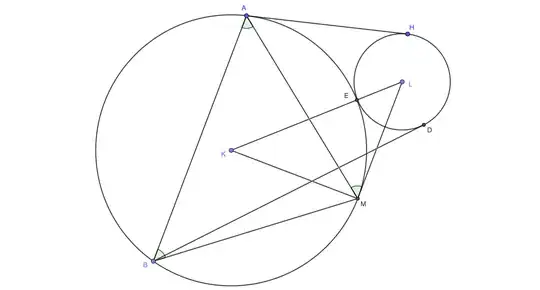
In the figure below, with $F$ as the intersection of the tangent at $E$ with tangent $LM$, it is clear by symmetry that tangent $CBFD$ passes through center $K$.
Since hypotenuse $KL=2KM$, then $\angle MKL=60^o$.
And since $\angle FKL=\angle KLF=30^o$, therefore exterior $\angle KFM=60^o$.
Further, since $\angle AKB= 90^o-30^o=60^o$, then $\triangle AKB$ is equilateral, $$\angle ABK=60^o=\angle KFM$$and$$LM\parallel AB$$And it is clear in this case that $M$ is the midpoint of arc $AMB$.