$\def\InvT{\operatorname{InvT}}$Introduction:
For some background information on the Dottie number D, see the great posts at:
Some definitions:
inverse beta regularized function $\text I^{-1}_x(a,b)$, beta regularized function $\text I_x(a,b)$, and the incomplete beta function $\text B_x(a,b)$: $$\text B_x(a,b)=\int_0^x t^{a-1} (1-t)^{b-1}dt, \text I_x(a,b)=\frac{\int_0^x t^{a-1} (1-t)^{b-1}dt}{\int_0^1 t^{a-1} (1-t)^{b-1}dt } =\frac{\text B_x(a,b)}{\text B(a,b)}$$ $$\text I_y(a,b)=x\implies y=\text I^{-1}_x(a,b);a,b>0,0\le x\le 1$$ where the restrictions on $x,a,b$ help find the quantile of a beta type distribution. There is also the Student t quantile $\InvT(x=\text{area},d=\text{degrees of freedom})$ in statistics from the Student t distribution: $$\text T(x,d)\mathop=^\text{def}\frac1{\sqrt d\text B\left(\frac d2,\frac12\right)}\int_{-\infty}^{x}\left(\frac{t^2}d+1\right)^{-\frac{d+1}2}dt=\frac12\left(1+\operatorname{sgn}(x)\text I_\frac {x^2}{x^2+d}\left(\frac d2,\frac12\right)\right)\\\text T(y,d)=x\implies y=\InvT(x,d),d>0$$ The goal is to notice that: $$\text B_x\left(\frac12,\frac32\right)=\int_0^x \sqrt{\frac 1t-1}dt=\sqrt{x-x^2}+\sin^{-1}\sqrt x\implies\text B\left(\frac12,\frac32\right)\text I_{\sin^2(x)}\left(\frac12,\frac32\right)\mathop=^{0\le x\le \frac\pi2}x+\frac12\sin(2x)$$ Therefore: $$\pi\operatorname I_{\sin^2\left(\frac x2-\frac\pi4\right)}\left(\frac12,\frac32\right)-\frac\pi2=x-\cos(x)=0\implies x=\text D=\frac \pi2-2\sin^{-1}\sqrt{\text I^{-1}_\frac12\left(\frac 12,\frac 32\right)}=\sin^{-1}\left(1-2 \text I^{-1}_\frac12\left(\frac 12,\frac 32\right)\right) $$ which is the inverse half covered sine. Using $\text D=\cos^{-1}(\text D)$ we get a perfect approximation with this computation. Finally, $\text I^{-1}_x\left(\frac12,b\right)$ is expressible via $\InvT(x,d)$ as in section 7 here. These give us closed forms:
The Main Result:
$$\boxed{\text{Dottie Number}=\text D=\text{hacoversin}^{-1}\,\text I^{-1}_\frac12\left(\frac 12,\frac 32\right)=\sqrt{1-\left(2\text I^{-1}_\frac12\left(\frac 12,\frac 32\right)-1\right)^2}=-\tanh\left(2\tanh^{-1}\left(\frac1{\sqrt3} \InvT\left(\frac14,3\right)\right)\right)=-\frac{2\sqrt3\InvT\left(\frac14,3\right)}{\InvT^2\left(\frac14,3\right)+3}}$$ where $\sqrt{\text{quantile}(1-\text{quantile})}$ is not quite a statistical formula. Also, $\text I^{-1}_\frac12(a,b)$ finds the median of a beta Distribution with $a,b$ as shape parameters.
Statistical Note:
Therefore we have a closed forms for the following special cases:
Median of $\frac 2\pi \sqrt{\frac 1x-1}$: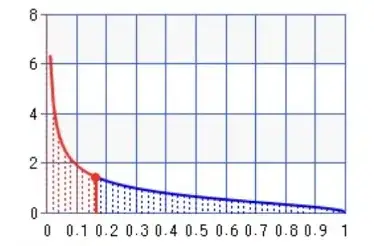 
where the median is the point such that half of the area of a curve is the red region and the other half is the blue region. The $\color{red}{\text {red}}$ horizontal line is the median:
$$\text{median}=\text I^{-1}_\frac12\left(\frac12,\frac32\right)=\frac {\text D_\text{DHA}^2}4=\text{hacoversin}(\text D)= \frac{1-\sqrt{1-\text D^2}}2=0.16319398540839259232…\implies \int_0^{\frac {\text D_\text{DHA}^2}4} \sqrt{\frac1x-1}\,dx=\int_0^{\text I^{-1}_\frac12\left(\frac12,\frac32\right)} \sqrt{\frac1x-1}\,dx=\frac\pi4 $$
where $\text D_\text{DHA}= \sqrt{1+\text D} - \sqrt{1-\text D} = \sqrt 2\sqrt{1-\sqrt{1-\text D^2}} $ is the offset at which $2$ unit disks overlap by half of each’s area constant. Notice how the Dottie number appears in the offset when a unit disk is half over another one and the median, where the areas from $0$ to the median is half of the area under the curve, of a beta distribution.
$1$st quartile of $\frac{6\sqrt3}{\pi(x^2+3)^2}$: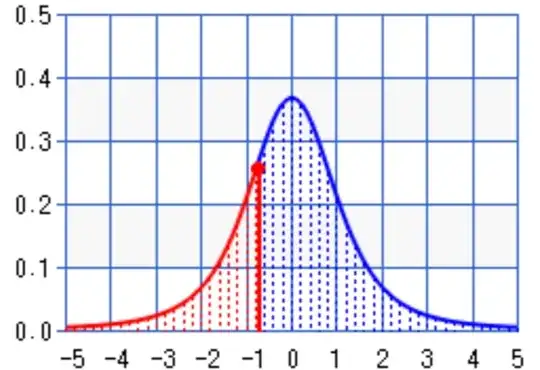 
where the 1st quartile, in $\color{red}{\text{red}}$ is the point such that $\frac14$ of the area of a curve is the red region and the other $\frac34$ is the blue region. Also, here the coversine appears:
$$1\text{st quartile}=\InvT\left(\frac14,3\right)=-\sqrt3\tanh\left(\frac12\tanh^{-1}(\text D)\right)=-\frac{\sqrt3\text{coversin}(\text D)}{\text D}= -\frac{\sqrt3\text D}{\sqrt{1-\text D^2}+1}= -0.764892328404345280657545\dots\implies\int_{-\infty}^{\InvT\left(\frac14,3\right)}\frac{dx}{(x^2+3)^2}=\frac{\pi}{24\sqrt3}$$
Power Series:
We use $\text I^{-1}_x(a,b)$’s series and Quantile Mechanics section $3.3$ to get another series expansion of the Dottie number: $$\begin{aligned}\text D=\text{hacoversin}^{-1}\sum_{n=1}^\infty a_n \left(\frac\pi8\right)^{2n} =\sqrt{1-\left(-1+2\sum_{n=1}^\infty a_n \left(\frac\pi8\right)^{2n}\right)^2}\\a_n=\frac1{(2n-1)(n-1)}\sum_{k=2}^{n-1} a_ka_{n-k+1}k(n-3k+2)+\sum_{k=1}^{n-1}\sum_{m=1}^{n-k}a_ka_ma_{n-k-m+1}k(2k-1)\\a_n=\left\{1,\frac13,\frac{11}{45},\frac{73}{315},\frac{3548}{14175},\frac{136883}{467775},\frac{15360178}{42567525},\frac{26838347}{58046625},\frac{59574521252}{97692469875},\frac{7635110149532}{9280784638125},\dots \right\}\end{aligned}$$ the Heaviside theta function from $3.3$ is unnecessary as the first sum is $0$ when $n=2$. The recurrence relation simplifies majorly from Quantile Mechanics, so possibly the double sum can become a single sum. Alternatively, the Student t quantile expresses the Dottie number and gives a series using Quantile Mechanics section $3.2$: $$\begin{aligned}\text D=- \tanh\left(2\tanh^{-1}\left(\frac1{\sqrt3} \InvT\left(\frac14,3\right)\right)\right)=-\frac{2\sqrt3\InvT\left(\frac14,3\right)}{\InvT^2\left(\frac14,3\right)+3}, \InvT\left(\frac14,3\right)= \sum_{n=0}^\infty a_n \left(\frac{\sqrt3\pi}8\right)^{2n+1}\\a_n=\frac1{3n(2n+1)}\sum_{k=0}^{n-1}\sum_{m=0}^{n-k-1}a_ka_ma_{n-k-m-1}(2(2m+1)(2n-2k-2m-1)-k(2k+1))=\left\{1,\frac29,\frac{11}{135},\frac{292}{8505},\frac{3548}{229635},\frac{273766}{37889775},\frac{15360178}{4433103675},\frac{214706776}{126947968875},\frac{59574521252}{71217810538875},\frac{15270220299064}{36534736806442875},\dots\right\}\end{aligned}$$ Both series are demonstrated here
The Question: Even though the calculations are an explanation, what is the intuition/interpretation behind the Dottie number being equal to the median of a beta distribution with half integer shape parameters or the $1$st quartile of a Student t distribution with $3$ degrees of freedom as described in the question?
