I have a set of data that has actual frequency. I have difficulty to find the method of building the negative binomial distribution model. How to relate the parameters in negative binomial distribution with the data?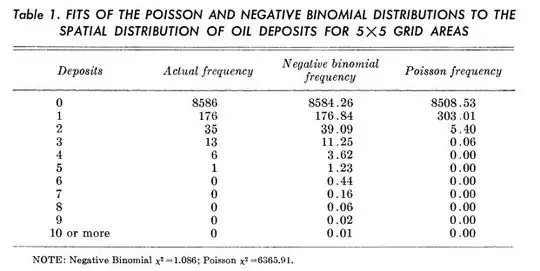
- 45
-
There are various methods for such a fit, including the method of moments. You need to choose the right structure for the negative binomial – Henry Feb 23 '22 at 13:43
-
The reading mention that the data are lognormally distributed. However I have problem to transform the log(0), meanwhile I need to calculate the variance. – Dara Feb 23 '22 at 13:47
-
Counts (especially counts of zero) are not lognormally distributed – Henry Feb 23 '22 at 13:51
-
Oh, yes. I am sorry, you're right. I read the wrong passage. The lognormal distribution is for the previous part. – Dara Feb 23 '22 at 14:02
-
I've tried to find alpha and beta using the method like this https://math.stackexchange.com/questions/185352/finding-alpha-and-beta-of-beta-binomial-model-via-method-of-moments and I make binomial distribution. Can these parameters (alpha and beta) obtained from that method be applied also for negative binomial distribution? However, I'm still confused to solve the combination of -r and k in the formula. – Dara Feb 23 '22 at 16:08
1 Answers
It is possible to reproduce the results in the table.
You can find the mean of the data is $0.03561302$ and the variance (without a Bessel correction) is $0.06156488$, so overdispersed compared to a Poisson distribution.
Since the mean of a negative binomial distribution is $\frac{(1-p)r}{p}$ and the variance is $\frac{(1-p)r}{p^2}$, the method of moments could suggest using $\hat p=0.5783977$ and $\hat r=0.04887077$. While these parameters are useful, they are not particularly meaningful in themselves: in the standard construction of the negative binomial, $r$ is the number of successes when you stop so a positive integer, but since they are just curve-fitting they might have ignored that point and that this $hat r$ is very small.
Using R to do the calculations, you then get
n <- 0:10
counts <- c(8586, 176, 35, 13, 6, 1, 0, 0, 0, 0, 0)
m <- sum(n * counts) / sum(counts)
v <- sum(n^2 * counts) / sum(counts) - m^2
phat <- m / v
rhat <- m^2 / (v - m)
c(m=m, v=v, phat=phat, rhat=rhat)
# m v phat rhat
# 0.03561302 0.06156488 0.57846328 0.04887077
cbind(n=n,
actual=counts,
negbin=round(dnbinom(n, rhat, phat) * sum(counts), 2),
poisson=round(dpois(n, m)* sum(counts), 2) )
# n actual negbin poisson
# 0 8586 8584.26 8508.53
# 1 176 176.84 303.01
# 2 35 39.09 5.40
# 3 13 11.25 0.06
# 4 6 3.62 0.00
# 5 1 1.23 0.00
# 6 0 0.44 0.00
# 7 0 0.16 0.00
# 8 0 0.06 0.00
# 9 0 0.02 0.00
# 10 0 0.01 0.00
which seems to match the numbers in the table
- 169,616
-
Thank you very much! I have forgot to include the actual frequency when calculating the variance, I used count(table row) as the denominator instead. I also tried using small number of r in Excel but it wouldn't work unless the r is more than or equal to one. Muchas gracias.. – Dara Feb 24 '22 at 00:37