Find number of ways to make a necklace (or a garland) consisting of $6$ identical diamonds and $3$ identical pearls.
I got the correct answer $7$ by taking different cases but when I applied the formula for arrangement, i.e. $$\frac{(6+3-1)!}{6!3!2}$$ I get a value which is not an integer. I divided by $6!$ and $3!$ because the diamonds and pearls are identical. Further I divided by $2$ since a necklace can be viewed from two sides.
Why am I getting a wrong answer?
Necklaces are invariant under rotation, while bracelets are invariant under rotation and reflection. You seem to be counting bracelets rather than necklaces.
If we arrange six indistinguishable diamonds and three indistinguishable pearls in a row, there are $\binom{9}{3}$ ways to select the positions of the pearls. We can join the ends of the row together to form a circle. Since there are nine objects, it would appear that there are nine linear arrangements which correspond to the same circular arrangement, once for each of the nine places we could cut the circle to obtain a linear arrangement, which would give $$\frac{1}{9}\binom{9}{3}$$ necklaces. However, this is not quite right because we can only divide by $9$ if each of the nine linear arrangements is distinct. As Ned pointed out in the comments, this is not true since there are only three distinct linear arrangements corresponding to the necklace in which each pair of pearls is separated by exactly two diamonds. Those linear arrangements are PDDPDDPDD, DPDDPDDPD, and PPDPPDPPD. Hence, dividing by $9$ counts that symmetrical necklace $1/3$ times. We want to count it once, so we must add $2/3$ to the total. Hence, there are $$\frac{1}{9}\binom{9}{3} + \frac{2}{3} = 10$$ distinct necklaces that can be formed with six indistinguishable diamonds and three indistinguishable pearls. They are shown below.
As Ned pointed out in the comments, you cannot simply divide the number of necklaces by $2$ to obtain the number of bracelets since some bracelets are their own reflections, so you would be counting each symmetrical bracelet $1/2$ times rather than once.
Notice that the four necklaces in the top row are symmetrical with respect to the vertical axis drawn through the top pearl. Thus, each of these four necklaces is its own reflection. Each necklace which is its own reflection produces one bracelet.
On the other hand, reflecting each necklace in the second row in this axis produces a different necklace, namely the necklace in the third row in the corresponding column. Each pair of necklaces which can be obtained by reflection from each other corresponds to a single bracelet.
Hence, the number of bracelets which can be formed using six indistinguishable diamonds and three indistinguishable pearls is $$4 + \frac{6}{2} = 4 + 3 = 7$$
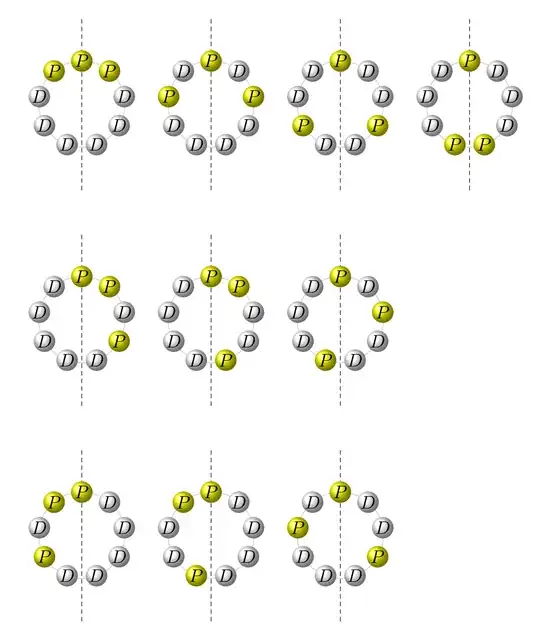
There are two possibilities here, rotational symmetry (necklace) or dihedral symmetry (bracelet). This is the OEIS naming convention. For the first one we have the cycle index of the cyclic group:
$$Z(C_n) = \frac{1}{n} \sum_{d|n} \varphi(d) a_d^{n/d}.$$
For second one we have the cycle index of the dihedral group
$$Z(D_n) = \frac{1}{2} Z(C_n) + \begin{cases} \frac{1}{2} a_1 a_2^{(n-1)/2} & n \text{ odd} \\ \frac{1}{4} \left( a_1^2 a_2^{n/2-1} + a_2^{n/2} \right) & n \text{ even.} \end{cases}$$
We get for $n=9$ the cycle indices
$$Z(C_9) = 1/9\,{a_{{1}}}^{9}+2/9\,{a_{{3}}}^{3}+2/3\,a_{{9}}$$
and
$$Z(D_9) = 1/18\,{a_{{1}}}^{9}+1/9\,{a_{{3}}}^{3}+1/3\,a_{{9}} +1/2\,a_{{1}}{a_{{2}}}^{4}.$$
Then by the Polya Enumeration Theorem we require
$$[D^6 P^3] Z(C_9; D+P)$$
and
$$[D^6 P^3] Z(D_9; D+P).$$
We thus get for the first case
$$\frac{1}{9} {9\choose 6} + \frac{2}{9} {3\choose 2} = 10$$
and the second one
$$\frac{1}{2} 10 + \frac{1}{2} [D^6 P^3] (D+P) (D^2+P^2)^4 \\ = 5 + \frac{1}{2} [D^6 P^2] (D^2+P^2)^4 + \frac{1}{2} [D^5 P^3] (D^2+P^2)^4 \\ = 5 + [D^3 P] (D+P)^4 = 5 + \frac{1}{2} {4\choose 3} = 7.$$
