Note: I have simplified the question. I think trying to generalise this straight away is biting off more than I can chew.
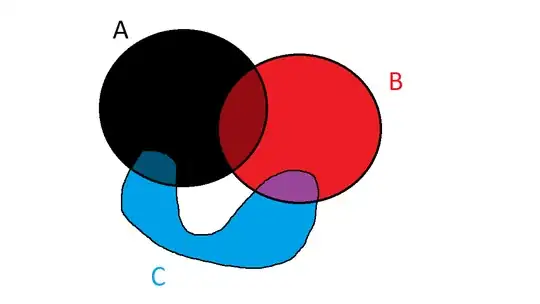
If $\ A, B, C\ $ are pairwise not disjoint, compact, connected subsets of $\ \mathbb{R}^2\ $ with $\ A \cap B \cap C = \emptyset\ $ then $\ \left(A\cup B\cup C\right)^c\ $ is disconnected. Is this true? Example diagram:
Note that if we did not require $\ A, B, C\ $ to be compact, and therefore closed, then $\ A = B'(\ (-1,0);\ 2\ ), B = B'(\ (1,0);\ 2\ ), C = \overline{B'(\ (0,10),\ 10-\sqrt{3})}\ $ where $\ B'(\ x;\ r)\ $ means the open ball centred at $\ x\ $ with radius $\ r,\ $ is an example where $\ \left(A\cup B\cup C\right)^c\ $ is not disconnected.