Does
$$ \int_{0}^{\infty} \sin (x^3) \, dx $$
converge? And If it does, why?
Does
$$ \int_{0}^{\infty} \sin (x^3) \, dx $$
converge? And If it does, why?
not a solution
Graphical evidence of convergence:
$$
\int_0^X \sin(x^3)\;dx
$$
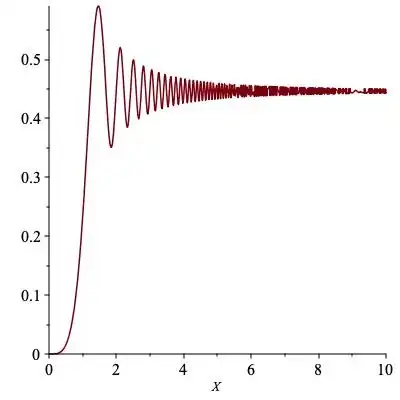
Added: this is correct, verified by Wolfram Alpha:
https://www.wolframalpha.com/input/?i=graph+integral%28sin%28x%5E3%29%2Cx%3D0..X%29%3B+from+X%3D1+to+10