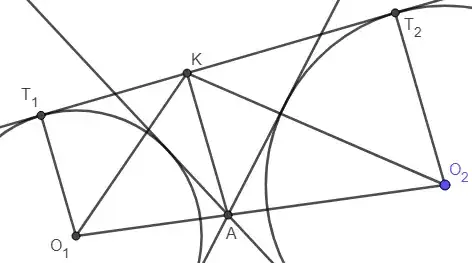
Given two disjointed circles $c_1$ and $c_2$, external to each other, let $A$ be the meeting of their internal tangents and let $K$ be the orthogonal projection of $A$ in one the common external tangents between $c_1$ and $c_2$. Prove that $AK$ bissects angle $O_1KO_2$.
I managed to solve it by realizing that $\frac{KT_1}{KT_2} = \frac{r_1}{r_2}$, which clearly solves the problem when one look at $\triangle O_1T_1K$ and $\triangle O_2KT_2$. But this problem seems to have a simpler solution. What do you think?