Equilateral triangle and very peculiar inscribed tangent circles

Question

The problem is to find the length of the size of the equilateral triangle below

I found one equation:

Let $R$ be the radius of the big circle whose red arc touches the two purple circles.

Let $A$ be the triangle vertex on which the red circle touches the green side. Let's call $B$ the other vertex of the green side. So in side $AB$ I've found this equation:

$x = \sqrt 3 + 2\sqrt R$

and that's it. I know we can think about a couple homotheties between the circles but they didn't seem much productive to me in order to find a new equation for $x$ and $R$. How to find a new equation or how to draw this figure?

EDIT: I can't prove it, but apparently one of the inner tangents of the purple circles is parallel to the green side.

EDIT2: It is quite similar to this question here in which we need to prove the internal tangent of the circles are parallel to one side of the triangle. Apparently it is not so trivial the application of the theorem mentioned in the answer to that question though.

Answer 1

Interesting problem! It's easy when you realize the equivalency between the images shown below.

Going to the second diagram from the first one is trivial using the parallel tangent theorem.

However, this is not a famous theorem.

Therefore, we may prove it for this special case.^$\star$

Consider:

We use Casey's theorem to achieve this.

Applying the theorem for $O,A,B,\Phi_1$ and $O,A,B,\Phi_2$ we have,

$$OA\cdot BK_1+OR_1\cdot AB=OB\cdot AT_1$$ $$OA\cdot BK_2+OR_2\cdot AB=OB\cdot AT_2$$

Subtracting first from the second gives $OA=OB$. (Note that $K_1K_2=T_1T_2$ and $OR_1=OR_2$.)

Similarly, we use Casey's theorem for $O,C,\Phi_1,D$ and $O,C,D,\Phi_2$ to get,

$$OC\cdot DQ+OD\cdot CQ=OR_1\cdot CD$$ $$OC\cdot DP+OR_2\cdot CD=OD\cdot CP$$

which gives $OC=OD$.

Thus we conclude $AB\parallel CD\parallel OR_2$.

Therefore in our picture (2^nd above) horizontal line (tangent) is parallel to the green side of the triangle. By symmetry, other inner tangent, and obviously, the external tangents of two purple circles are parallel to the corresponding sides of the triangle.

$\square$

---

For the interested readers, 'parallel tangent theorem' says,

Consider two circles $\Phi_1$ and $\Phi_2$ tangent to a circle $\Phi$ (internally/externally). Let $O$ be the point where $\Phi$ intersects the radical axis of $\Phi_1$ and $\Phi_2$. Then the tangent to $\Phi$ that passes throught $O$ is parallel to the external/internal (depends upon the configuration of three circles) tangent of $\Phi_1$ and $\Phi_2$ that lies on the same side of the chord created by the intersection of external tangents ($AB$) as $O$.

^$\star$ The same method can be applied to prove the general case.

References:

• Two Applications of the Generalized Ptolemy Theorem: https://www.jstor.org/stable/2695499

• https://mathoverflow.net/q/284458

Answer 2

One approach is to place the figure on a coordinate plane so that $A = (0,0)$, and $|AB| = 2s$. Then if the radius of the red circle is $R$, we can show that the following points are expressible in terms of $s$ and $R$:

• The center of the red circle, which we will call $O$, is located at $(0,R)$.
• The center of the purple circle tangent to the green line, which we will call $P$, is $(2s - \sqrt{3}, 1)$.
• The center of the purple circle internally tangent to the red circle, which we will call $Q$, is $(s, s \sqrt{3} - 2)$.

Then observe $|OP| = R+1$ and $|OQ| = R-1$. So by the Pythagorean theorem, we obtain $$\begin{align} s^2 + (R - (s \sqrt{3} - 2))^2 &= (R-1)^2, \\ (2s - \sqrt{3})^2 + (R-1)^2 &= (R+1)^2. \end{align}$$

Solving this system for $R, s$ is left as an exercise for the reader, and yields the desired radius of the red circular arc and half the side length of the equilateral triangle, and the full side length is $2s$.

Answer 3

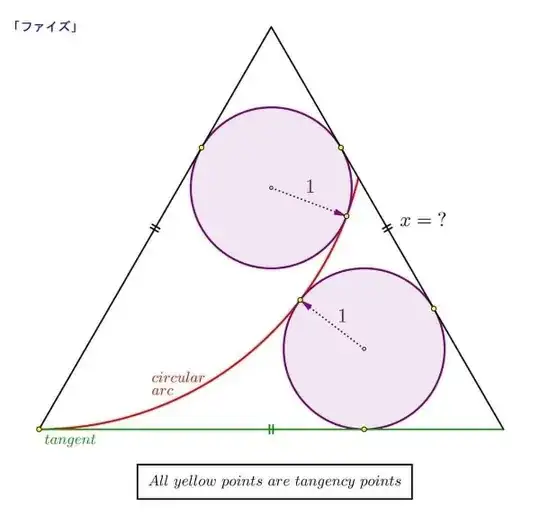
On the picture below, $M$ is the midpoint of $AB$ and so $AM$ is the orthogonal bisector of $BC$. Reflection with respect to $AM$ sends $C$ to $B$ and circle $c_1$ to circle $c_2$, i.e. these are symmetric with respect to $AM$. Under the reflection, the image the circle $c$ is denoted by $c^{*}$ and since $c$ is tangent to both $c_1$ and $c_2$, so is $c^{*}$. Moreover, since $c$ is tangent to $AB$, its symmetric image $c^{*}$ is tangent to $AC$.

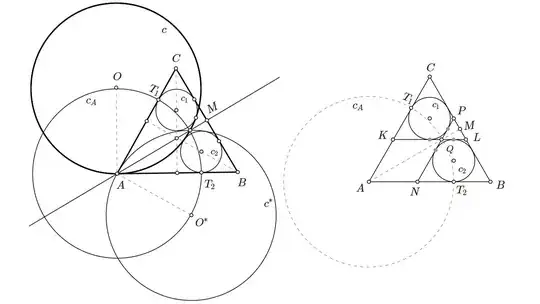
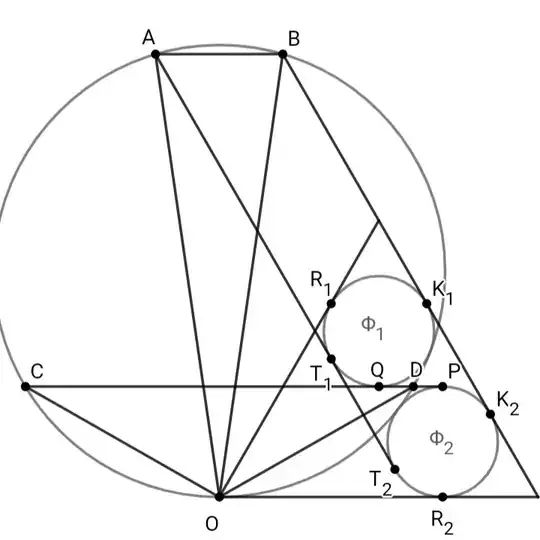
Consider the circle $c_A$ centered at $A$ and with radius $AT_1 = AT_2$, where $T_1$ and $T_2$ are the points of tangency of $c_1$ and $c_2$ with $AC$ and $AB$ respectively. Perform inversion with respect to the circle $c_A$. By construction, circles $c_1$ and $c_2$ are mapped to themselves. By the properties of inversions, the circles $c$ and $c^{*}$ passing through the center $A$, are mapped to straight lines. In addition to that, since $c$ is tangent to $c_1$ and $c_2$, its inverse image is a line, tangent to both $c_1$ and $c_2$, i.e. it is a common inner tangent of the circles $c_1$ and $c_2$. Moreover, since $c$ is tangent to $AB$, and since after inversion $AB$ is mapped to itself, the inverse image of $c$ is a line parallel to $AB$. All of the facts form above combined yield the conclusion that the inverse image of the circle $c$ with respect to the circle $c_A$ is a common inner tangent line of the two circles $c_1$ and $c_2$, which in addition to that, is parallel to $AB$.

Analogously, by symmetry, the inverse image of the circle $c^{*}$ with respect to the circle $c_A$ is the other common inner tangent line of the two circles $c_1$ and $c_2$, which is parallel to $AC$.

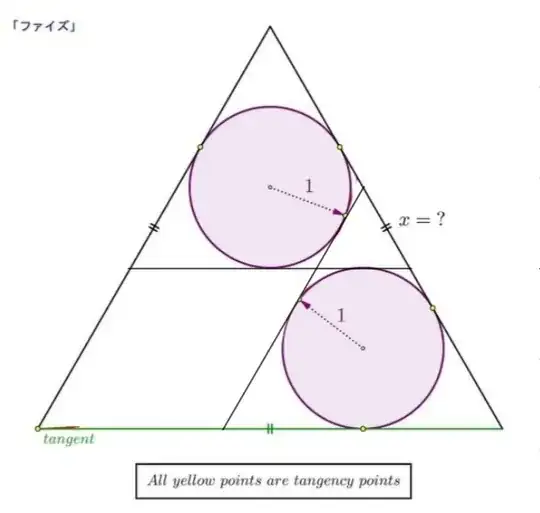
So the result of the inversion is depicted on the right, where the inverse images of the circles $c$ and $c^{*}$ are the lines $KL$ and $NP$ which are also the common inner tangents of $c_1$ and $c_2$, parallel to $AB$ and $AC$ respectively. $Q$ is the intersection point of $KL$ and $NP$ and by symmetry, must lie on $AM$. (Remark: $c, \, c^{*}$ and $AM$ are not concurrent and point $Q$ is actually not on $c_A$. It just looks like they are.)

Since $KL \, || \, AB$ and $NP\,||\,AC$ and, the quads $CKQP$ and $BNQL$ are symmetric, congruent, isosceles trapezoids with $60^{\circ}$ and $120^{\circ}$ angles. Furthermore, since the circles $c_1$ and $c_2$ are inscribed in the trapezoids $CKQP$ and $BNQL$ of radius $1$, their diameters are $2$ and since their diameters are also the altitudes of the trapezoids $CKQP$ and $BNQL$. The latter leads to the fact that

$$AN = NQ = BL = AK = KQ = CP = \frac{4}{\sqrt{3}}$$ If we denote $x = AB = BC = CA$, then $$LQ = PQ = LP = x - BL - CP = x - \frac{8}{\sqrt{3}}$$ and $$BN = CK = x - AK = x - AN = x - \frac{4}{\sqrt{3}}$$ The property of having $c_2$ as a circle inscribed in $BNQL$ is equivalent to the identity $$BN + LQ = NQ + BL$$ which leads to the equation $$x - \frac{4}{\sqrt{3}} \, + \, x - \frac{8}{\sqrt{3}} \, = \, \frac{4}{\sqrt{3}} + \frac{4}{\sqrt{3}}$$ $$2\,x - \frac{12}{\sqrt{3}} \, = \, \frac{8}{\sqrt{3}}$$ $$x - \frac{6}{\sqrt{3}} \, = \, \frac{4}{\sqrt{3}}$$ so $$AB = BC = CA = x = \frac{10}{\sqrt{3}} = \frac{10}{3}{\sqrt{3}}$$