0

I'm learning about Fourier transforms and watching this video.

The instructor says that if a frequency exists in a sound, we will get a non-zero coefficient using Fourier transform and a zero coefficient for the frequencies not in the sound.

Let's look at these examples:

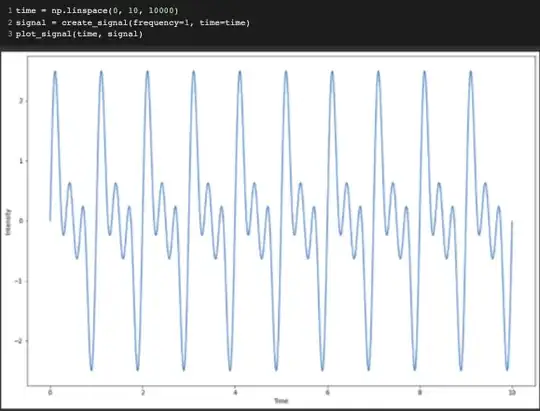
This is our signal with a frequency of 1

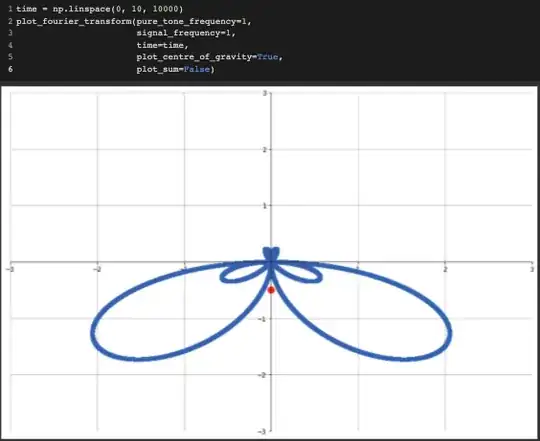
enter image description here

This is the Fourier transform for frequency 1 (which is in the sound):

enter image description here

As we can see, the centre of gravity(the average of all points)is a non-zero value.

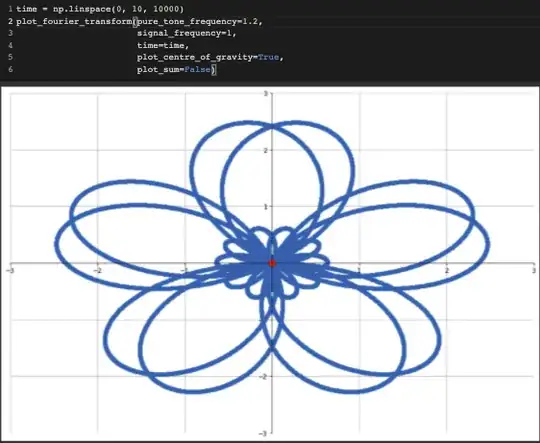
But for a frequency not in the sound (for example, 1.2), we get a symmetric shape, and the average of all points become zero.

enter image description here

The formula for calculating the coefficient is this: $ \huge{ \hat{g}(t) = \int {g(t) e^{-i2\pi ft}} dt} $

Where f is the frequency, we're checking, and t is time.

Why do we get a symmetric shape for the frequencies not in the sound (therefore a zero centre of gravity) and a non-symmetric shape for frequencies based on this formula?

Morez
  • 103
  • 1
    What happens if you take $g(t) = e^{i 2 \pi f t}$ in the integral? What if you take $g(t) = e^{i 2 \pi f' t}$ for some other $f' \neq f$? – Jakob Streipel Jan 01 '22 at 18:16
  • 1
    (That aside: note that pictures shouldn't be a central part of questions here, if it can be helped, since they aren't accessible as text. You may wish to have a look at MathJax.) – Jakob Streipel Jan 01 '22 at 18:18
  • for the first part, we get $\e^0 in the integral which gives us t and for the second one we get $\e^i(f'-f)*2*pi*t! – Morez Jan 01 '22 at 18:43
  • Yes. Now the integral as written in the question is missing some bounds. What if you evaluate those from $0$ to $1$? – Jakob Streipel Jan 01 '22 at 18:43
  • in that case, we would just have $ e^ {i(f'-f)2pi} $ for the second one and 0 for the first one – Morez Jan 01 '22 at 18:45
  • Not quite, since we evaluate at $1$ and at $0$ and subtract. – Jakob Streipel Jan 01 '22 at 18:51
  • 1
    The short answer to your "why?" question is "the orthogonality of sin()/cos() of one frequency with the sin()/cos() of a different frequency". Orthogonality means that integrals such as $\int_{-T/2}^{T/2} \cos(2\pi m t)\cos(2\pi nt) dt = 0$ for $m\ne n$. – Andy Walls Jan 01 '22 at 19:29

1 Answers1

2

A frequency $f$ being present in the signal $g(t)$ means that we can decompose $g(t)$ into a bunch of terms, one of which is (some scalar multiple of) $e^{2 \pi i f t}$.

Now the Fourier transform of this signal is $$ \int_0^1 e^{2 \pi i f t} e^{-2 \pi i f t} \, d t = \int_0^1 1 \, d t = 1. $$

On the other hand, if we try this with some frequency not present in the signal, say $f' \neq f$, we get $$ \int_0^1 e^{2 \pi i f' t} e^{-2 \pi i f t} \, d t = \int_0^1 e^{2 \pi i (f' - f) t} \, d t = \frac{e^{2 \pi i (f' - f) t}}{2 \pi i (f' - f)} \biggr\rvert_0^1 = 0. $$

Note that the integral in the opening post (and in the video) is missing the bounds of integration, which in this case are very important.

Jakob Streipel
  • 1,859
  • That makes sense but as far as I'm aware, Fourier transform is between $ -\infty $ and $ \infty $. And another question is that why the shapes we get is a symmetric shape for frequencies not in the signal? – Morez Jan 01 '22 at 18:54
  • This is the exact formula from wikipedia: $ {\displaystyle {\hat {f}}(\xi )=\int _{-\infty }^{\infty }f(x)\ e^{-2\pi ix\xi },dx,\quad \forall \ \xi \in \mathbb {R} .} $ – Morez Jan 01 '22 at 18:55
  • 1
    @Morez Your question was specifically about the Fourier coefficients of a periodic signal, so the bounds of the integrals are over an integral number of periods (usually 1 period of the fundamental frequency) to get a Fourier coefficient of a Fourier Series. Using the continuous Fourier Transform with a periodic signal requires consideration of distributions/generalized functions. – Andy Walls Jan 01 '22 at 19:25
  • This and the various answers and comments might be interesting further reading. – Jakob Streipel Jan 01 '22 at 19:30
  • Great, Thanks for the answer and also introducing MathJax! – Morez Jan 01 '22 at 19:36