Comparing Factorials vs 2^n

Question

I have the following question: In general, is $N!$ bigger than $2^N$?

Using the R programming language, I made a plot of these $N!$ vs $2^N$:

library(ggplot2)
library(cowplot)
original_number = c(0:50)
 factorials = factorial(original_number)
 two_to_the_power = 2 ^  original_number
 table = data.frame( original_number,factorials, two_to_the_power)
head(table)
original_number factorials two_to_the_power
1               1          1                2
2               2          2                4
3               3          6                8
4               4         24               16
5               5        120               32
6               6        720               64
g1 = ggplot(table, aes( original_number )) + 
  geom_line(aes(y =  two_to_the_power, colour = " two_to_the_power")) + 
  geom_line(aes(y =  factorials, colour = "factorials")) + ggtitle("Which is Bigger: Factorials or 2^n?")
g2 = ggplot(table, aes( original_number )) + 
  geom_line(aes(y =  log(two_to_the_power), colour = " two_to_the_power")) + 
  geom_line(aes(y =  log(factorials), colour = "factorials")) + ggtitle("Which is Bigger: Factorials or 2^n? (Log Scale)")
plot_grid(g1, g2)

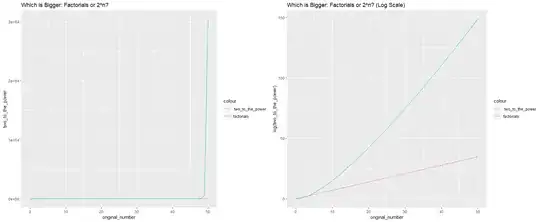
Based on this plot, it seems that $N!$ is initially smaller, bu soon $N!$ becomes far bigger than $2^N$.

My Question: Suppose I did not have a calculator or a computer to plot these graphs - are there any "tricks" in math that could have been used to see which of these is bigger?

I believe you meant to say that $2^n$ is initially bigger, but $n!$ soon grows way bigger than $n!$. — Alan Abraham, Dec 30 '21 at 07:58
https://math.stackexchange.com/questions/76946/prove-the-inequality-n-geq-2n-by-induction — Gary, Dec 30 '21 at 08:00
"it seems that $N!$ is initially bigger, but $2^N$ soon grows way bigger than $N!$" $;-;$ That's the opposite of what the graph you posted shows. Think of it, if you multiply $2$ to itself $N$ times, how do you expect it to compare vs. multiplying an ever increasing sequence of numbers from $1$ to $N$ the same number of times? — dxiv, Dec 30 '21 at 08:04
If you just want to prove $n!>2^n$ for $n\ge 4$, you can use induction. That $n!>>2^n$ for large $n$ can easily be seen by considering that we get the next entry of the sequence $\frac{n!}{2^n}$ by multiplying with $\frac{n+1}{2}$ , which gets bigger in each step. — Peter, Dec 30 '21 at 09:08

5xum · Accepted Answer · 2021-12-30T08:06:37.207

Based on this plot, it seems that N! is initially bigger, but 2^N soon grows way bigger than N!.

Then your plot is wrong, or better yet, you just misread it or you mistyped what you wanted to say.

In general, you have

$$N! = 1\cdot 2\cdot 3\cdot 4\cdots\cdot N > 1\cdot 2\cdot 3\cdot 3\cdot 3\cdots 3 = 2\cdot 3^{N-2}$$

so $2^N$ will be smaller. Indeed, the same line of reasoning can be used to prove that $N!$ is bigger than $a^N$ for any $a\in\mathbb R$.

More precisely, the idea of the proof above shows the statement:

For any $b\in\mathbb R$, there exists some $c\in\mathbb R$ such that, for large enough values of $N$, we have $N! > c\cdot b^N$.

This also means that, for any $a\in\mathbb R^n$, we have

$$\lim_{n\to\infty}\frac{a^n}{n!} = 0$$ because, for large values of $n$, we have (if we take $b=a+1$):

$$\frac{a^n}{n!} < \frac{a^n}{c\cdot (a+1)^n} = \frac1c\cdot \left(\frac{a}{a+1}\right)^n,$$

and $$\lim_{n\to\infty} \left(\frac{a}{a+1}\right)^n = 0.$$

Comparing Factorials vs 2^n

1 Answers1