It is well known that under a certain condition (e.g. the weak convergence), the convergence of norms implying the convergence in norm, that means
Theorem. (see e.g. MSE) In a Hilbert space $\mathcal H$, let $x_n$ be a sequence weakly converging to $x$. If $||x_n|| \rightarrow ||x||$ then $x_n$ converges to $x$ in norm, i.e. $||x_n-x||\rightarrow 0$.
I am wondering that is there a similar result for Minkowski functional? (a.k.a. gauge function, block norm in combinatorics, atomic norm in signal processing). I mean: is there a sufficient condition such that the following statement holds true?
Statement. For $x_n\in \mathcal H$, if $||x_n||_A \rightarrow ||x||_A$, then $||x_n-x||_A\rightarrow 0$.
Here $A$ is a closed convex set (not necessarily bounded) in $\mathcal H$ containing the origin as its interior point and $||\cdot||_A$ is the Minkowski functional corresponding to $A$, i.e. $||x||_A := \inf \{t\geq 0: x\in t A\}$ for all $x\in \mathcal H$.
Of course, this statement is not true even in $\mathcal H=\mathbb R^2$ if we don't impose any condition, indeed, see the counter example given in the following figure.
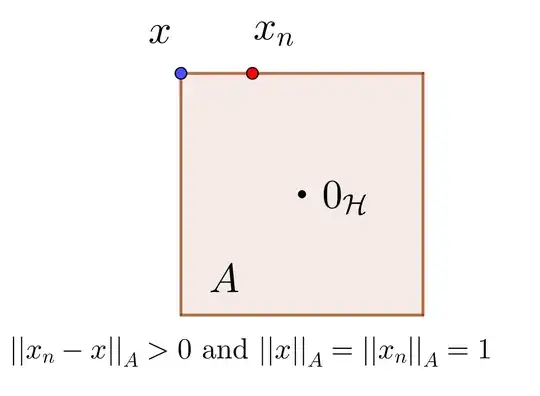
Is there any ideas?